TD 2021 PHYSIQUE

ENNONCE

Partie I : Évaluation des ressources / 24 points

Exercice 1 : Vérification des savoirs / 8 points

1.1. Définir: phénomène périodique, radioactivité. (2pt)
1.2. Énoncer: la loi d'attraction universelle, la deuxième loi de Newton sur le mouvement. (2pt)
1.3. La période d'un pendule simple est donnée par la relation \(T = 2\pi \sqrt {\frac{l}{g}} \) Indiquer les grandeurs physiques qui interviennent dans cette relation et donner leurs unités dans le système international. ( 2 pts)
1.4. Répondre par vrai ou faux :
(i). Lorsqu'on modifie l'amplitude d'une vibration sinusoïdale, sa période change. (1 pt)
(ii). Le mouvement d'une particule chargée dans un champ électrique uniforme est toujours rectiligne uniforme. (1 pt)

Exercice 2 : Application des savoirs / 8 points

Les parties 1, 2 et 3 sont indépendantes

Partie 1 : 0nde progressive / 2 points

Une pointe animée d'un mouvement vibratoire sinusoïdal transversal de fréquence 20 Hz provoque la naissance des ondes à partir d'un point O de la surface de l'eau. La distance entre deux rides consécutives est de 60 mm.
1.1. Déterminer la longueur d'onde du mouvement. (1pt)
1.2. Déterminer la célérité de l'onde dans ce milieu. (1pt)

Partie 2 : Source radioactive / 3 points

La demi-vie d'un noyau radioactif est 1,0 seconde.
2.1. Calculer sa constante de désintégration \(\lambda \). (1 pt)
2.2. A l'instant initial t = 0, un échantillon a une activité radioactive égale à \(1,11 \times {10^8}\) Bq.
Déterminer son activité à la date t = 3,0 s. (2 pts)

Partie 3 : Force de Lorentz / 3 points

Reproduire les schémas et représenter la force de Lorentz qui s'exerce sur la particule dans les cas suivants: (3pt)

Exercice 3 : Utilisation des savoirs / 8 points

A- Uniquement la série TI / 8 points

Les parties A1 et A2 sont indépendantes

A.1. Champ électrique / 4 points

En deux points A et B, on place respectivement deux charges \({q_A}\) et \({q_B}\). On considère un point M du segment \(\left[ {AB} \right]\) situé à 4,0 cm de A.
A.1.1. Représenter le champ électrique créé par \({q_A}\) en M, puis déterminer son module sachant que \({q_A} = + 0,4\mu C\) (2 pts)
A.1.2. Déterminer \({q_B}\) pour que le champ électrique résultant soit nul au point M. (2 pt)
Données : AB = 6,0 cm ; \(k = 9,0 \times {10^9}\) SI; \(1\mu m = {10^{ - 6}}m\)

A.2. Effet photoélectrique / 4 points

Un faisceau lumineux monochromatique, de longueur d'onde \(\lambda = 0,40\mu m\), est dirigé sur la cathode d'une cellule photoélectrique au césium. Le seuil photoélectrique du césium correspond a une longueur d'onde \({\lambda _0} = 0,66\mu m\).
A.2.1. Déterminer l'énergie d'extraction d'un électron. (1 pt)
A.2.2. Déterminer l'énergie du photon incident. (1 pt)
A.2.3. Déterminer l'énergie cinétique maximale d'un électron émis. (2 pt)
Données : vitesse de la lumière dans le vide : \(C = 3,0 \times {10^8}\) m/s ; constante de Planck :
\(h = 6,2 \times {10^{ - 34}}\) J ; \(1\mu m = {10^{ - 6}}m\)

B Uniquement la série D / 8 points

Les parties B.1 et B.2 sont indépendantes

B.1. Fentes de Young / 4 points

On désire retrouver la longueur d'onde d'une source lumineuse monochromatique au laboratoire d'un établissement scolaire avec le dispositif des fentes de Young. Dans ce dispositif la source S éclaire deux fentes secondaires \({{S_1}}\) et \({{S_2}}\) distantes de a. La source S est située sur la médiatrice de \({{S_1}{S_2}}\). L'écran d'observation E est parallèle au plan et situé à une distance D de ce plan.
B.1.1. Faire le schéma légendé de l'expérience permettant de visualiser des franges d'interférences. (1pt)
B.1.2. La différence de marche ô entre les rayons issus des fentes sources \({{S_1}}\) et \({{S_2}}\) est donnée par la relation \(\delta = \frac{{ax}}{D}\) en un point M d'abscisse x comptée à partir du milieu de la frange centrale.
Donner la condition que doit vérifier \(\delta \) pour que le point M apparaisse brillant. (1pt)
B.1.3. Montrer que l’interfrange est donné par la relation \(i = \frac{{\lambda D}}{a}\). (1pt)
B.1.4. On mesure la distance correspondant à 2 interfranges et on trouve d = 9,5 mm.
Déterminer la longueur d'onde de cette source. (1pt)
Données : a = 0,20 mm; D = 1,50 m.

B.2 Satellite / 4 points

Le mouvement d'un satellite (S) de masse ms, est étudié dans le référentiel géocentrique considéré galiléen. La Terre est assimilée à une sphère homogène de masse \({M_T}\) de rayon \({R_T}\) et de centre O. La période de rotation de la Terre autour d'elle-même est notée T. Le satellite est assimilable à un point matériel se déplaçant d'un mouvement uniforme sur une trajectoire de rayon \(r = {R_T} + h\), h étant l'altitude du satellite.
B.2.1. Donner l'expression de l'intensité F de la force gravitationnelle s'exerçant sur le satellite en fonction \({m_s}\), \({M_T}\) h et G (constance gravitationnelle). ( 2 pt)
8.2.2. En utilisant le théorème du centre d'inertie, déterminer l'expression de la vitesse linéaire du satellite. ( 2 pt)

Partie II: Évaluation des compétences / 16 points

Situation problème:

Pour acheminer certaines billes de bois, une société forestière opte pour la voie fluviale. C'est ainsi qu'une bille de bois de masse \(m = 1,5 \times {10^3}\) kg est poussée le long d'une pente inclinée d'un angle \(\alpha = {11^0}\), par un engin exerçant une force constante parallèle à la ligne de plus grande pente du plan incliné. En B, la bille de bois amorce une descente et arrive dans le fleuve.
A l'instant t = 0 s, le centre d'inertie G de la bille coïncide avec le point O et est au repos. Le point
O est l'origine de l'axe (x’x) parallèle à la pente, et orienté vers le haut (figure ci-dessous).
On admet que la bille glisse sans rouler.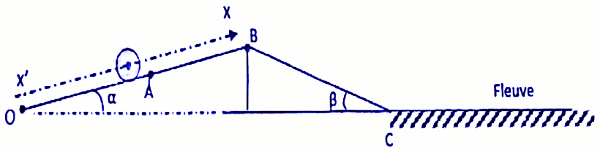
Première phase (de O à A)
Entre les points O et A distants de d = 80 m, l'engin exerce une force motrice d'intensité F sur la bille. Celle-ci est alors animée d'un mouvement uniformément varié d'accélération \(\overrightarrow a \). Elle arrive en A avec une vitesse d'intensité \({V_A} = 16\) m/s.
Deux élèves de terminale voulant évaluer la force motrice sont en désaccord sur sa valeur. L'un propose 5262 N et l'autre 6984 N.
On néglige les forces de frottements

Deuxième phase (de A à B)
Arrivée au point A, les ouvriers règlent (grâce à un dispositif approprié) la force motrice de l'engin à une nouvelle valeur \(F' = 9,2 \times {10^3}\) N. La résultante des forces de frottements \(\overrightarrow f \) a pour intensité \(f = 7,5 \times {10^3}\) N. Entre A et B, la bille animée d'un mouvement décéléré arrive au point B avec une vitesse nulle.
Le Directeur Général offre une prime spéciale à tous les acteurs de la deuxième phase si celle-ci se fait en moins de 22 s.
Données : g =10 m/s2
1. En exploitant les informations de la première phase, départage les deux élèves. (10 pts)
2. En vous appuyant sur la deuxième phase du mouvement de la bille et à l'aide d'une démarche scientifique, vérifie si les acteurs de la deuxième phase bénéficieront de la prime. (6 pts)

CORRECTION

Partie I : Évaluation des ressources

Exercice 1 : Vérification des savoirs / 8 points

1.1. Définitions
Phénomène périodique : c'est un phénomène qui se répète identiquement à des intervalles de temps successifs, réguliers et égaux appelés période T. 1 pt
Radioactivité : transformation spontanée d'un noyau instable en un autre noyau avec émission d'une particule et d'un rayonnement électromagnétique. 1 pt
1.2. (1 pt)
• La loi d'attraction universelle: deux corps ponctuels A et B de masses respectives m, et ma s'attirent mutuellement g les forces d'attraction sont directement opposées, dirigées suivant la droite (AB), d'intensité commune proportionnelle à leurs masses et inversement proportionnelle au carré de la distance qui les sépare.
\(\overrightarrow {{F_{A/B}}} = - \overrightarrow {{F_{B/A}}} = \) \(\frac{{G{m_A}{m_B}}}{{A{B^2}}}\overrightarrow u \)
G est la constante gravitationnelle et \(\overrightarrow u \) un vecteur directeur unitaire de la droite (AB). 1 pt
• La deuxième loi de Newton sur le mouvement : Dans un référentiel galiléen, la somme vectorielle des forces extérieures appliquées à un solide est égale au produit de la masse du solide par le vecteur accélération de son centre d'inertie G. 1 pt
\(\sum {\overrightarrow {{F_{ext}}} = m.\overrightarrow {{a_G}} } \)
1.3. Période d'un pendule simple : \({T_0} = 2\pi \sqrt {\frac{l}{g}} \) 2 pts
T\({T_0}\) : période en seconde (s); \(l\) : longueur du pendule en mètre (m); g: intensité de la pesanteur du lieu en mètre par seconde carre (m/s2) ou en newton par kilogramme (N/kg)
1.4.
(i). Faux 1 pt
(il). Faux 1 pt

Exercice 2 : Application des savoirs / 8 points

Parle 1 : Onde progressive

1.1. Longueur d'onde
La distance entre deux rides consécutives correspond à la longueur d'onde:
\(\lambda = 60\) mm = 0,060m 1 pt
1.2 Célérité de l’onde
\(\lambda = \frac{C}{N} \Rightarrow C\) \( = \lambda N = 1,2\) m/s 0,5 x 2= 1 pt

Partie 2 : source radioactive

2.1 Constance de désintégration \(\lambda = \frac{{\ln 2}}{T} = 0,69\) s^-1 0,5 x 2 = 1 pt
2.2 Activité
Loi de décroissance
\(A(t) = {A_0}\exp \left( { - \lambda t} \right)\) \( \Rightarrow A(3) = \) \({A_0}\exp \left( { - 3\lambda } \right) = \) \(1,4 \times {10^7}\) Bq 2 pts

Partie 3 : Force de Lorentz

Représentation de la force de Lorentz qui s’exerce sur la particule dans les cas suivants :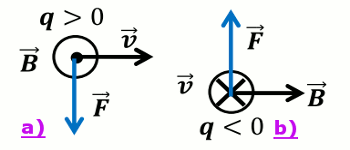

Exercice 3 : Utilisation des savoirs

A-Uniquement la série TI

Les parties A1 et A2 sont indépendantes

A.1. Champ électrique

A.1.1- Représentation du vecteur champ créé par \({q_A}\) en M
Représentation du vecteur champ \(\overrightarrow {{E_A}} \left( M \right)\) 1 pt
Module du champ électrique produit par \({q_A}\) au point M 2 pts
\({E_A}(M) = \) \(\frac{{k\left| {{q_A}} \right|}}{{A{M^2}}} = \) \(2,25 \times {10^6}\) V/m
A.1.2 Valeur de \({q_A}\) 2 pts
Le vecteur champ créé par les sources \({q_A}\) et \({q_B}\) au point M est tel que
\(\overrightarrow E (M) = \overrightarrow {{E_A}} (M)\) \( + \overrightarrow {{E_B}} (M) = \overrightarrow O \) \( \Rightarrow {E_A}(M) = \) \({E_B}(M) \Leftrightarrow \) \(\frac{{k\left| {{q_A}} \right|}}{{A{M^2}}} = \frac{{k\left| {{q_B}} \right|}}{{B{M^2}}}\)
Ainsi \(\left| {{q_B}} \right| = \left| {{q_A}} \right|\) \(\frac{{{{\left( {AB - AM} \right)}^2}}}{{A{M^2}}} = \) \(0,1\mu c\)
Puisque les deux vecteurs champ sont directement opposés, \({q_B}\) est positive
\({q_B} = {10^{ - 7}}C\)

A.2. Effet photoélectrique

A.2.1- Énergie d’extraction d’un électron. 1 pt
\({W_0} = \frac{{hc}}{{{\lambda _0}}}\) \( = 1,88eV\)
A.2.2- Énergie du photon incident. 1 pt
\(W = \frac{{hc}}{\lambda } = 3,10eV\)
A.2.3- Énergie cinétique maximale d’un électron émis. 2 pts
\({E_{{C_{\max }}}} = W - {W_0}\) \( = 1,956 \times {10^{ - 19}}J\)

B-Uniquement la série D

B.1. Fentes de Young
B.1.1. Schéma légendé de l’expérience permettant de visualiser des franges d’interférences. 1 pt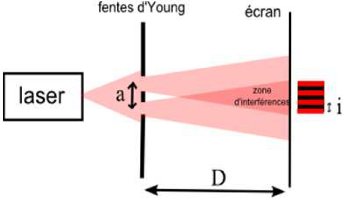
B.1.2. La condition que doit vérifier δ pour que le point M apparaisse brillant \(\delta = k\lambda \) avec \(k \in \mathbb{Z}\) 1 pt
B.1.3- Montrons que l’interfrange est donné par la relation \(i = \frac{{\lambda D}}{a}\) 1 pt
• Pour des franges brillantes
\({x_k} = \frac{{k\lambda D}}{a}\) \( \Rightarrow {x_{k + 1}} = \) \(\frac{{\left( {k + 1} \right)\lambda D}}{a}\)
Ainsi \(i = {x_{k + 1}} - {x_k}\) \( = \frac{{\lambda D}}{a}\)
B.1.4- Longueur d’onde de cette source.
\(d = \frac{i}{2} = \) \(\frac{{\lambda D}}{{2a}} \Rightarrow \lambda \) \( = \frac{{2ad}}{D}\)
AN : \(\lambda = 2,5 \times {10^{ - 6}}\) m
B.2. satellite
B.2.1- Expression de l’intensité F de la force gravitationnelle s’exerçant sur le satellite en fonction de m s , \({M_T}\), \({R_T}\) , h et G (constance de gravitationnelle). 2 pts
\(F = \frac{{G{M_T}{m_S}}}{{{{\left( {{R_T} + h} \right)}^2}}}\)
B.2.2- En utilisant le théorème du centre d’inertie, déterminons l’expression de la vitesse linéaire du satellite.
Force appliquée : force de gravitation \(\overrightarrow F \) exercée par Saturne sur le satellite.
Théorème du centre d’inertie
\(\overrightarrow F = m\overrightarrow {{a_G}} \)
Ainsi \(\overrightarrow F = \frac{{G{M_T}{m_S}}}{{{{\left( {{R_T} + h} \right)}^2}}}\overrightarrow u \) \( = {m_S}\overrightarrow {{a_G}} \) (1)
Avec \(\overrightarrow {{a_G}} \left\{ \begin{array}{l}{a_t} = 0\\{a_N} = \frac{{{V^2}}}{{{R_T} + h}}\end{array} \right.\), le movement du satellite est circulaire uniforme d’ou \({a_t} = 0\)
De la relation (1)
\({a_N} = G\frac{{{M_T}}}{{{{\left( {{R_T} + h} \right)}^2}}}\) \( = \frac{{{V^2}}}{{{R_T} + h}}\)
\(V = \sqrt {\frac{{G{M_T}}}{{{R_T} + h}}} \)

Partie Il : Évaluation des compétences

1. Il s'agit d'évaluer la force motrice F de l'engin lors de la première phase afin de se prononcer sur les déclarations des deux élèves.
Pour cela, nous allons :
(i) Déterminer l'accélération du mouvement en utilisant les relations cinématiques
(ii) Appliquer le théorème du centre d'inertie pour déterminer la force motrice
(iii) Comparer la valeur obtenue aux valeurs proposées, puis conclure.
Accélération du mouvement :
La bille est animée d'un mouvement rectiligne uniformément varié
\(V = {a_G}t \Rightarrow \) \(x = \frac{1}{2}{a_G}{t^2} \Rightarrow \) \({a_G} = \frac{{{V^2}}}{{2x}}\)
(A t= 0M, x=0 et V=0)
Au point A, \({a_G} = \frac{{V_A^2}}{{2d}}\)
Application du TCI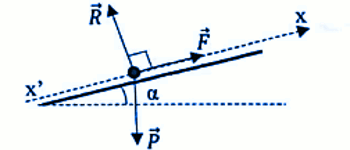
Référentiel terrestre supposé galiléen.
Forces extérieures appliquées à la bille de bois: son poids \(\overrightarrow P \), la réaction \(\overrightarrow R \) du support et la force motrice \(\overrightarrow F \).
Le TCI s'écrit : \(\overrightarrow P + \overrightarrow F + \) \(\vec R = m\overrightarrow {{a_G}} \)
Suivant x'x : \(F = mg\sin \alpha \) \( + m{a_G}\) soit
\(F = mg\sin \alpha \) \( + m\frac{{V_A^2}}{{2d}}\)
A.N : F= 5261 N
Comparaison et conclusion : la valeur obtenue est égale à celle du premier élève. Donc le premier élève a raison.
2. Il s'agit d'évaluer la durée de la deuxième phase afin de prévoir si les ouvriers bénéficieront d'une prime.
Pour cela, nous allons :
(i) Appliquer le TCI au mouvement de la bille pour déterminer l'accélération
(Iii) Utilisons l'équation horaire de la vitesse pour déduire la durée recherchée:
(iii) Comparer la durée obtenue à 22s, puis conclure.
Application du TCI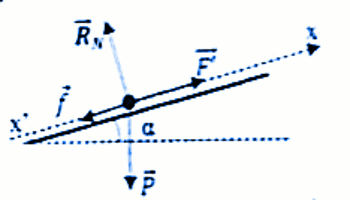
Référentiel terrestre suppose galiléen.
Forces extérieurs appliquées à la bille de bois : son poids \(\overrightarrow P \), la réaction normale \({\overrightarrow R _N}\), du support, la force de frottement \(\overrightarrow f \) et la force motrice \(\overrightarrow F \).
Le TCl s’écrit: \(\overrightarrow P + \overrightarrow F’ + \) \({\overrightarrow R _N} + \overrightarrow f = \) \(m\overrightarrow {{a_G}} \)
Suivant x'x : \( - mg\sin \alpha + F’\) \( - f = m{a_G}\)
Soit : \({a_G} = - g\sin \alpha \) \( - \frac{f}{m} + \frac{{F'}}{m}\)
A.N: \({a_G} = - 0,775\) m/s²
Équation horaire de la vitesse : \(V = {a_G}t + {V_A}\)
Au point B : \({V_B} = 0\) \( \Rightarrow {a_G}t + {V_A} = 0\)
\({t_B} = \frac{{{V_A}}}{{{a_G}}}\) \( = 20,6s\)
Comparaison et conclusion : \({t_B} = 20,6s\) est inférieure à 22 s.
Donc les acteurs de cette deuxième phase bénéficieront de la prime spéciale accordée par le directeur Général.