ENNONCE
Exercice 1 : Champs de forces et mouvement dans les champs de forces / 7 points
Les trois parties sont indépendantes
Partie 1. Mouvement d'un projectile / 3 points
Pour atteindre une cible circulaire de-rayon R = 50 cm, disposée verticalement à une distance D = 2 m de O, on lance des billes à la même vitesse \({\vec v_0}\); de valeur \({v_0}\),. Le centre O’ de la cible est sur la même horizontale que O (Voir figure ci-dessous).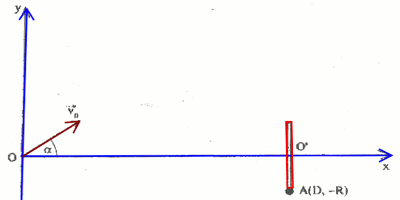 On suppose la bille ponctuelle et on néglige l'action de l'air. On donne g = 9.8 m/s2.
On suppose la bille ponctuelle et on néglige l'action de l'air. On donne g = 9.8 m/s2.
1. En appliquant le théorème du centre d'inertie à l'une des billes lancées, déterminer dans le repère (Ox, Oy) les équations horaires de mouvement de celle-ci. A 1pt
2. En déduire dans le même repère, l'équation de la trajectoire de la bille en fonction de \({v_0}\), g et \(\alpha \) l'angle d'inclinaison de la vitesse de lancement de la bille par rapport à l'horizontale. 1pt
3. Lorsqu'on lance une bille de telle sorte que sa vitesse soit horizontale, celle-ci touche la cible en un point A de coordonnées \(\left( {{x_A} = D;{y_A} = - R} \right)\) sur la verticale de O'. Calculer la valeur de la vitesse de lancement vo de la bille. 1pt
Partie 2 : La sonde Pioneer 11 au voisinage de Jupiter / 2,5 points
Jupiter est la planète système sa plus massive du solaire. Ses caractéristiques physiques sont :
rayon moyen : \({R_J} = 70 \times {10^3}\)km ;
masse : \({M_J} = 1,9 \times {10^{27}}\) kg ;
gravité à la surface : \(Go = 24,8\)m/s2.
On admet que Jupiter est un corps à distribution de masse à symétrie sphérique.
1. Exprimer l'intensité du champ de gravitation de Jupiter en un point N extérieur à la planète dont on notera la distance au centre de Jupiter r. 1,5pt
2. En notant z, la distance entre la surface de Jupiter et le point N, exprimer la valeur du champ de gravitation de Jupiter au point N de la question précédente en fonction de Go, de z et du rayon moyen de la planète. 1 pt
3. Calculer l'intensité de la force que Jupiter exerçait sur la sonde Pioneer 11 de masse 300 kg, qui la survola en 1974 à 42 000 km de sa surface. 1pt
Partie 3 : Les lois de Newton sur le mouvement / 1,5 points
Énoncer deux lois de Newton sur le mouvement. 1,5pt
Exercice 2 : Systèmes oscillants / 4 points
Un pendule simple est constitué d'une masse ponctuelle suspendue à une ficelle de longueur \(l\) et de masse négligeable dont l'extrémité supérieure est fixée à un point fixe O.
Le pendule est mis en mouvement et un dispositif enregistre l'angle \(\theta \) que fait le fil du pendule avec la verticale du point de suspension O à chaque instant. L'enregistrement obtenu est donné à la figure 1 de l'annexe à remettre avec la copie. On néglige l'action de l'air. On prend g = 10 m/s2 ; on désigne par To la période propre des oscillations.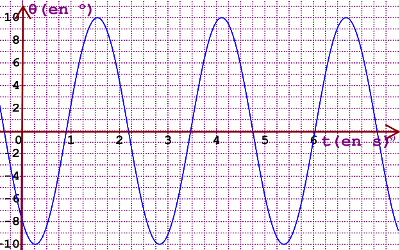 1. Faire le bilan des forces qui s'exercent sur la masse m à une date t quelconque. On fera un schéma. 0,5 pt
1. Faire le bilan des forces qui s'exercent sur la masse m à une date t quelconque. On fera un schéma. 0,5 pt
2. Établir l'équation différentielle du mouvement dans le cas des oscillations de faible amplitude. 1 pt
3. À l'aide de la figure 1 de l'annexe, déterminer la période propre des oscillations ainsi que leur amplitude. 0,75 pt + 0,5pt
4. Déduire de la valeur de To la longueur du fil du pendule. 0,5 pt
5. Écrire la loi horaire du mouvement du pendule 0,75pt
Exercice 3 : Les phénomènes ondulatoires et corpusculaires / 5 points
Les deux parties sont indépendantes ‘
A Phénomènes ondulatoires / 2,5 points
Une source S émettant une lumière monochromatique dont on veut déterminer la longueur d'onde \(\lambda \), éclaire une plaque percée de deux trous distants de \(a = 500\mu m\). Les deux trous sont placés à égale distance de la source et se comportent comme deux autres sources qui sont alors synchrones et cohérentes. Ce dispositif produit des interférences sur un écran à une distance D = 4 m de la plaque.
1. Expliciter le sens des expressions suivantes utilisées dans le texte d'introduction : 0,25 pt +0,5 pt
• lumière monochromatique ;
• sources cohérentes.
2. Définir l'interfrange. 0,5 pt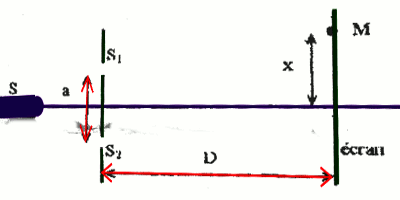 3. La distance séparant le milieu de la quatrième frange brillante à droite et celui de la cinquième frange brillante à gauche de la frange centrale est d = 45 mm. Donner l'expression de l'interfrange i, en fonction des caractéristiques du dispositif des trous d’ Young utilisé et de \(\lambda \), la longueur d'onde. Calculer la valeur de la longueur d'onde de la lumière utilisée. 0,5pt+0,75pt
3. La distance séparant le milieu de la quatrième frange brillante à droite et celui de la cinquième frange brillante à gauche de la frange centrale est d = 45 mm. Donner l'expression de l'interfrange i, en fonction des caractéristiques du dispositif des trous d’ Young utilisé et de \(\lambda \), la longueur d'onde. Calculer la valeur de la longueur d'onde de la lumière utilisée. 0,5pt+0,75pt
B. Phénomènes corpusculaires / 2,5 points
Une cellule photoélectrique, est montée en série avec un générateur de tension continue réglable et un microampèremètre. On éclaire la cellule avec une radiation monochromatique de longueur d'onde A dans le vide.
1. Définir l'effet photoélectrique. 0,5pt
2 Un photon d'énergie \({E_\lambda }\) arrivant sur la plaque de la cellule peut provoquer l'émission d'un électron d'énergie cinétique maximale \({E_C}\).
Écrire la relation qui existe entre \({E_C}\) et le potentiel d'arrêt Uo, puis la relation entre \({E_\lambda }\), \({E_C}\) et le travail d'extraction \({W_S}\) d'un électron. 0,5 pt + 0,5pt
3. On mesure le potentiel d'arrêt correspondant lorsque la cellule est éclairée par une radiation monochromatique de longueur d'onde \({\lambda _1} = 0,470\mu m\). On trouve U1 = 1,18 V.
Déterminer \({W_S}\) le travail d'extraction. En déduire \({\lambda _S}\), la longueur d'onde seuil photoélectrique de la cellule. 1 pt
On donne : la célérité de la lumière \(c = 3 \times {10^8}\) m/s; la valeur de charge élémentaire \(e = 1,6 \times {10^{ - 19}}\) C, la constante de Planck \(h = 6,62 \times {10^{ - 34}}\) J.s.
Exercice 4 : Exploitation des résultats d'une expérience / 4 points.
Le polonium est un élément radioactif rare de symbole Po. Il se désintégré en émettant des particules \(\alpha \).
1. Écrire l'équation traduisant la désintégration du noyau de Polonium 210.
On donne un extrait de la classification périodique : \({}_{81}Th\), \({}_{82}Pb\), \({}_{83}Bi\), \({}_{84}Po\), \({}_{85}At\). 0,5pt
2. Soit N(t) le nombre de noyaux radioactifs d'un échantillon de polonium, non désintégrés à la date t. A la date t = 0 on note No le nombre de noyaux radioactifs présents dans l'échantillon. Un détecteur de radioactivité associé à un compteur à affichage numérique permet d'effectuer les mesures regroupées dans le tableau ci-dessous :
| t(jours) | 0 | 40 | 80 | 120 | 160 | 200 | 240 |
| \(\frac{{N(t)}}{{{N_0}}}\) | 1,00 | 0,82 | 0,67 | 0,56 | 0,45 | 0,37 | 0,30 |
| \( - \ln \left[ {\frac{{N(t)}}{{{N_0}}}} \right]\) | 0,00 | 0,20 | 0,40 | 0,80 | 1,20 |
2.1. Calculer a et b. 0,5pt
2.2. Sur la figure 2 du document à remettre avec la copie, tracer la courbe des variations de \( - \ln \left[ {\frac{{N(t)}}{{{N_0}}}} \right]\) en fonction du temps.
On prendra pour échelle : En abscisse : 1 cm pour 15 jours ; En ordonnées : 1 cm pour 0,1. 1,5pt
3. Sachant que \(\ln \left( {{e^{ - \lambda t}}} \right)\) \( = - \lambda t\), peut-on dire que la loi de décroissance est en accord avec la représentation graphique précédente ? Justifier la réponse. 0,5 pt
4. Déterminer la pente de la courbe obtenue et en déduire la constante radioactive  caractéristique de l'isotope 210 du Polonium. 0,5pt
5. Donner l’expression de la demi-vie de l'échantillon notée \({t_{\frac{1}{2}}}\) et calculer sa valeur en jours. 0,5pt
CORRECTION
Exercice 1 : Mouvements dans les champs de forces / 7 points
Partie 1. Mouvement d’un projectile / 3 points
1. Équations horaires du mouvement 1 pt
Dans le référentiel terrestre supposé galiléen, une bille est soumise uniquement à son poids \(\vec p\) ; D’apres le TCI 0,25 x 2 = 0,5 pt
\(\sum {\overrightarrow {{F_{ext}}} = } m\overrightarrow a \)
Soit \(\overrightarrow a = \overrightarrow g \)
Par intégration, nous obtenons :
\(\vec v\left| \begin{array}{l}\dot x = {v_o}\cos \alpha \\\dot y = - gt + {v_o}\sin \alpha \end{array} \right.\)
Soit \(\overrightarrow {OG} \left| \begin{array}{l}x = {v_o}t\cos \alpha \\y = - \frac{1}{2}g{t^2} + {v_o}t\sin \alpha \end{array} \right.\) 0,25 x 2 = 0,5 pt
2. Équation de la trajectoire
De cette expression , \(x = {v_o}t\cos \alpha \), nous avons \(t = \frac{x}{{{v_o}\cos \alpha }}\) et cette relation dans l’expression en y nous permet d’avoir l’équation de la trajectoire
\(y = - \frac{1}{2}g\) \(\frac{{{x^2}}}{{v_0^2{{\cos }^2}\alpha }}\) \( + x\tan \alpha \) 0,5 pt x 2 = 1 pt
3. Valeur de la vitesse initiale
Comme la vitesse initiale est horizontale (\({\alpha = 0}\)), l’équation de la trajectoire s’écrit :
\(y = - \frac{1}{2}g\frac{{{x^2}}}{{v_0^2}}\)
Le point \(A\left( \begin{array}{l}D\\ - R\end{array} \right)\) appartient à la trajectoire, dont \( - R = - \frac{1}{2}g\frac{{{D^2}}}{{v_0^2}}\) \( \Rightarrow {v_o} = \) \(D\sqrt {\frac{g}{{2R}}} \) \( = 6,26\) m/s
Partie B : La sonde Pionner 11 au voisinage de Jupiter / 2,5 points
Expression de l’intensité du champ de gravitation au point N
Soit K la constante de gravitation universelle ; \(G(N) = \frac{{K.{M_f}}}{{{r^2}}}\) 0,5 pt
2. Valeur du champ de gravitation au point N
Comme \(r = {R_f} + z\) , on a : \(G(N) = \) \(\frac{{K.{M_f}}}{{{{\left( {{R_f} + r} \right)}^2}}}\) (?) ; par ailleurs, à la surface de Jupiter\({G_0} = \frac{{K.{M_f}}}{{{{\left( {{R_f}} \right)}^2}}}\) (2) 0,25 pt x 2
En combinant les relations (1) et (2), on obtient : \(G\left( N \right) = \) \({\left( {\frac{{{R_f}}}{{{R_f} + z}}} \right)^2}{G_0}\) 0,5 pt
3. Intensité de la force de gravitation \(F = mG\left( N \right)\); on obtient :
\(F = m{G_0}\) \({\left( {\frac{{{R_f}}}{{{R_f} + z}}} \right)^2}\); A.N. : \(F = 2,91 \times {10^3}\) N 0,5 pt x 2 = 1 pt
Partie 3 : Les lois de Newton sur le mouvement / 1,5 point
Énonces de deux lois de Newton sur le mouvement 0,75 pt x 2 =1,5 pt
• Première loi de Newton ou principe d’inertie : Dans un référentiel galiléen, lorsqu’un solide est isolé ou pseudo isolé, son centre d’inertie G est :
- Soit au repos, si G est initialement au repos ;
- Soit animé d’un mouvement rectiligne uniforme, si G est initialement en mouvement.
• Deuxième loi de Newton ou théorème du centre d’inertie : Dans un référentiel galiléen, la somme vectorielle des forces appliquées à un système est égale au produit de sa masse par le vecteur accélération de son centre d’inertie.
• Troisième loi de Newton ou principe d’interaction : Lorsqu’un corps (C) exerce sur un corps (C’) une force \({\overrightarrow F _{C/C'}}\), le corps C’ réagit et exerce simultanément sur le corps (C) une force \({\overrightarrow F _{C’/C}}\), de même direction, de même intensité et de sens contraire.
Exercice 2 : Systèmes oscillants / 4 points
1. Bilan des forces : 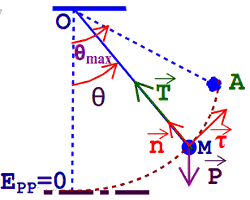 Système : le solide ponctuel, dans le référentiel terrestre.
Système : le solide ponctuel, dans le référentiel terrestre.
Forces appliquées :
• Le poids \(\overrightarrow P \) du solide ;
• La tension \(\overrightarrow T \)
2. Équation différentielle
2e loi de Newton : \(\sum {\overrightarrow {{F_{ext}}} = } m\overrightarrow {{a_G}} \) \( \Rightarrow \overrightarrow P + \overrightarrow T = \) \(m\overrightarrow {{a_G}} \) 0,25 pt
Par projection suivant l’axe tangentiel \(\left( {G;\overrightarrow t } \right)\) du repère de Frenet, on a , \( - g\sin \alpha = \frac{{dv}}{{dt}}\) avec, \(v = L\dot \theta \) ; d’où \(\ddot \theta + \frac{g}{L}\sin \theta \) 0,5 pt
Pour les faibles amplitudes, on a : \(\sin \theta \approx \theta \) et finalement \(\ddot \theta + \frac{g}{L}\theta = 0\) 0,25 pt
3. Période : \({T_0} = 2,56\) s ; amplitude : \({\theta _m} = {10^o}\) ?? \({\theta _m} = \frac{\pi }{{18}}\) ??? 0,75 pt+ 0,5 pt
4. Calcule de la longueur du fil ; partant de ? \({T_0} = 2\pi \sqrt {\frac{L}{g}} \), on obtient \({T_o} = 2\pi \sqrt {\frac{L}{g}} \) \( \Rightarrow L = \frac{{gT_0^2}}{{4.{\pi ^2}}}\); L = 1,66 m 0,25 pt x 2 = 0,5 pt
4. Équation horaire est de la forme \(\theta (t) = \) \({\theta _m}\cos ({\omega _0}t + \varphi )\) 0,25 pt
Conditions initiales : à t = 0 ; \({\theta _0} = - {8^0}\) et \(\dot \theta \prec 0\)
Comme \(\dot \theta (t) = - {\theta _m}{\omega _0}\) \(\sin ({\omega _0}t + \varphi )\) on a, à l’instant initial \(\left\{ \begin{array}{l} \cos \varphi = - \frac{4}{5}\\\sin \varphi \succ 0 \end{array} \right.\) \( \Rightarrow \varphi = 2,5\) rad 0,25 pt
La pulsation est \(\omega = \frac{{2\pi }}{T}\) \( = 2,45\) rad/s
Finalement \(\theta (t) = \frac{\pi }{{18}}\) \(\cos (2,45t + 2,5)\) en rad ou \(\theta (t) = 10\) \(\cos (2,45t + 2,5)\) en degré 0,25 pt
Exercice 3 : Les phénomènes ondulatoires et corpusculaires / 5 points
A- Phénomènes ondulatoires / 2,5 points
1. Sens des expressions
Lumière monochromatique : lumière constituée d’une seule couleur. 0,25 pt
Sources cohérentes : sources conservant entre elles un déphasage constant. 0,5 pt
2. L’interfrange est la distance séparant les milieux de deux franges consécutives de même nature. 0,5 pt
3. Expression de l’interfrange : \(i = \frac{{\lambda D}}{a}\) 0,50 pt
Calcul de la longueur d’onde : \(i = \frac{d}{9}\) \(i = \frac{{\lambda D}}{a}\) \(\lambda = \frac{{ad}}{{9D}}\) ; A.N. \(\lambda = 6,25 \times {10^{ - 7}}\)? 0,25 x 3 = 0,75 pt
B- Phénomènes corpusculaires / 2,5 points
1. Effet photoélectrique : émission d’électrons par un métal éclairé par un rayonnement électromagnétique convenable.
2. Relations
\(\left\{ \begin{array}{l}{E_C} = e{U_0}\\{E_\lambda } = {E_C} + {W_S}
\end{array} \right.\) 0,5 pt x 2 =1 pt
3. Détermination de \({W_S}\)
\({W_S} = {E_\lambda } - {E_C}\) \( = \frac{{h.c}}{{{\lambda _1}}} - \) \(e{U_1} = \) \(2,34 \times {10^{ - 19}}j\) 0,25 pt x 2 = 0,5 pt
Calcul de \({{\lambda _S}}\)
\({\lambda _S} = \frac{{h.c}}{{{W_S}}}\) \( = 8,5 \times {10^{ - 7}}\) ? 0,25 pt x 2
Exercice 4 : Exploitation des résultats d’une expérience / 4 points
1. Équation de la désintégration :
\({}_{84}^{210}Pu \to \) \({}_2^4He + \) \({}_{82}^{206}Pb\) 0,5 pt
2. Les nombres a et b sont les valeurs manquantes du tableau ;
2.1. Calcul de a et b : (?, ?? ; ?, ?? ) 0,25 pt x 2 = 0,5 pt
2.2. Tracé de la courbe des variations de \( - \ln \left[ {\frac{{N(t)}}{{{N_0}}}} \right]\) en fonction du temps. 1,5 pt 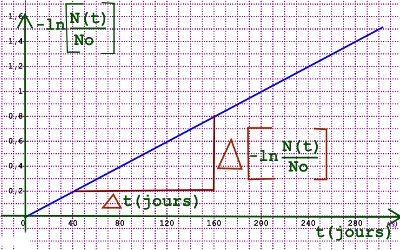 3 D’après la loi de décroissance radioactive, \(N(t) = {N_0}{e^{ - \lambda t}}\) , donc \( - \ln \left[ {\frac{{N(t)}}{{{N_0}}}} \right] = \lambda t\) ce qui correspond à une droite passant par l’origine. 0,25 pt
3 D’après la loi de décroissance radioactive, \(N(t) = {N_0}{e^{ - \lambda t}}\) , donc \( - \ln \left[ {\frac{{N(t)}}{{{N_0}}}} \right] = \lambda t\) ce qui correspond à une droite passant par l’origine. 0,25 pt
Comme la courbe obtenue est une droite passant également par l’origine, on peut dire que la loi de décroissance est en accord avec la représentation graphique réalisée. 0,25 pt
4. Pente p de la courbe :
\(p = \) \(\frac{{\Delta \left( { - \ln \left[ {\frac{{N(t)}}{{{N_0}}}} \right]} \right)}}{{\Delta t}}\) \( = 5 \times {10^{ - 3}}\) jour-1 0,25 pt
Constante radioactive \(p = \lambda = \) \(5 \times {10^{ - 3}}\) jour-1 0,25 pt
5. Demi-vie \({t_{\frac{1}{2}}} = \frac{{\ln 2}}{\lambda }\) \( = 138,6\) ????? 0,25 pt x 2 = 0,5 pt
Commentaires
Enregistrer un commentaire