ENNONCE
Exercice 1 : Mouvements dans les champs de force / 7 points
Les parties A et B sont indépendantes.
Partie A /3,5 points
Soit le dispositif ci-dessous où AM est une tige de cuivre mobile autour d'un axe horizontal \(\left( \Delta \right)\) perpendiculaire au plan de la figure et passant par A. La tige AM baigne dans un champ magnétique-\(\overrightarrow B \) uniforme et son extrémité M plonge dans une cuve de mercure. On admettra que la longueur de la partie immergée dans le mercure est négligeable.
On ferme le circuit, la tige s'écarte alors de sa position d'équilibre initiale d'un angle \(\alpha \) vers la droite.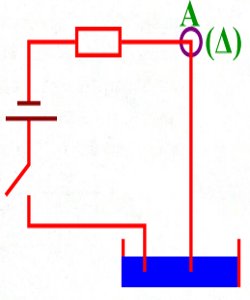 l-Représenter :
l-Représenter :
l-1-La force électromagnétique qui s'applique sur la tige en faisant ressortir le sens du champ magnétique. (On admettra que cette force électromagnétique \(\overrightarrow F \) est localisée au point C milieu de AM) 1 pt
I-2- Les autres forces qui s'appliquent sur AM. 0,5 pt
2- Écrire les conditions d'équilibre de la tige. 0,5 pt
3- En déduire l'expression de l'angle u en fonction de m, g, l, L, B, puis calculer sa valeur. 1+0,5pt
Prendre : m=40g; i=8A ; B = 0,025T; L=10cm; g=9,8m/s2.
Partie B / 3,5 points
Lors d'un corner, au cours d'un match des lions indomptables, EYOBO communique au ballon placé en un point O origine d'un plan (O ; x, y) vertical, une vitesse Vo=20m/s faisant un angle \(\alpha = {60^o}\) avec l'horizontale (Voir figure ci-dessous).0n admettra que l'action de l'air sur le ballon, considéré comme un solide ponctuel est négligeable et que l'accélération de la pesanteur dans ce stade est g=9,8 m/s2.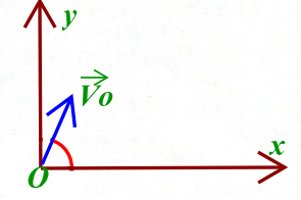 1- Définir la chute libre. 0,5pt
1- Définir la chute libre. 0,5pt
2- Appliquer le théorème du centre d'inertie au ballon et déterminer les lois horaires du mouvement. 1,5pt
3- En déduire l'équation de sa trajectoire. 0,5 pt
4- Calculer la distance \(O{X_P}\), ou \({X_P}\) est le point de chute du ballon sur le plan horizontal. 1 pt
Exercice 2 : Systèmes oscillants /4 points
Le graphe \(\theta = f(t)\) représenté dans la figure ci-dessous, traduit les variations de l’élongation d'un pendule simple en fonction du temps.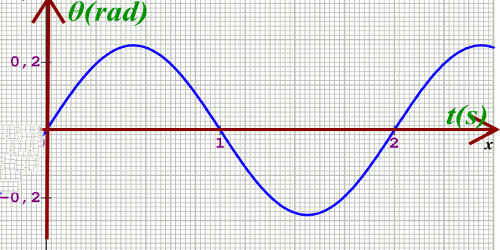 1- Faire le schéma annoté d'un pendule simple. 0,5 pt
1- Faire le schéma annoté d'un pendule simple. 0,5 pt
2- En exploitant ce graphe, déterminer :
2-1-la période, l'amplitude maximale des osclllations.et l’élongation initiale de ce pendule. 1,5pt
2-2- En déduire l'expression de l'élongation du pendule en fonction du temps. 1 pt
2-3-Sachant que ce pendule simple a une longueur de 1 m, déterminer la valeur de l'accélération de la pesanteur en ce lieu. 1 pt;
Exercice 3 - Phénomène ondulatoire et corpusculaires / 5 points
Les parties A et B sont Indépendantes.
Partie A / la lumière (2.5 ponts)
Une source de lumière monochromatique S éclaire deux sources secondaires S1 et S2 distants de a=3mm. La source S est placée sur la médiatrice de S1S2. On place un écran d'observation à la distance D=3m du plan des sources secondaires. Les plans contenant S, S1S2 et E sont parallèles
1- indiquer sur un schéma, la zone de l'écran où sont observées les franges d'interférences 1 pt
2- La distance séparant la 3eme frange brillante située avant la frange centrale et la 3eme brillante après la frange centrale est de 4,2 mm,
2-1- Calculer l’interfrange. 0,75 pt
2-2- En déduire la longueur d'onde de la radiation utilisée. 0,75 pt
Partie 8/ Radioactivité (2,5 points)
Le radium \({}_{88}^{226}Ra\) se désintègre suivant la réaction : \({}_{88}^{226}Ra \to \) \({}_y^xRn + {}_2^4He\)
1- Donner la signification des nombres 226 et 88. 0,5 pt
2- Donner une application de la radioactivité. 0,5 pt
3- Déterminer x et y. 0,5 pt
4- Calculer en MeV, l'énergie libérée lors de la désintégration d'un noyau de radium. 1 pt
Données : masse du noyau de radium : 225,9771 u
masse du noyau de radon : 221,3704 u
masse du noyau d'hélium : 4,0015 u
1u = 931,5 Mev/c2
EXERCICE 4 : Expérience de physique / 4 points
L'objectif de cet exercice est de déterminer l'énergie minimale d'extraction \(Wo\) d'un électron d'un métal constituant la cathode d'une cellule photoélectrique.
Pour ce faire, on éclaire cette cellule avec différentes radiations de fréquence N et on mesure les potentiels d'arrêt correspondants. On obtient les résultats suivants :
| \(N( \times {10^{14}}Hz)\) | 5,5 | 6,2 | 6,9 | 7,5 | 8,4 |
| \(Uo(V)\) | 0,20 | 0,49 | 0,79 | 1.03 | 1,38 |
1- Définir : potentiel d'arrêt. 0,5 pt
2- Tracer la courbe \(N = f(Uo)\) Échelle : 1 cm pour \({10^{14}}\) Hz et 1cm pour 0,2 V. 1 pt
3- Donner la relation entre le potentiel d'arrêt et la fréquence de la radiation incidente.
Vérifier si cette relation est en accord avec le graphe obtenu. 1 pt:
4- Déduire du graphe la valeur de \(Wo\).On prendra \(h = 6,62 \times {10^{ - 34}}\) J.s 1,5 pt
Commentaires
Enregistrer un commentaire