ENNONCE
Exercice 1 : Mouvements dans les champs de force et leurs applications / 7 pointsLes parties A et B sont indépendantes.
Partie A : Solide en mouvement sur une piste / 4 points
Un solide (S) de masse m est lancé de A (qu'on prend comme origine des espaces), en haut d’un plan incliné infiniment long, avec une vitesse initiale \(\overrightarrow {{v_A}} \) . L’angle que fait le plan avec la verticale est noté \(\alpha \). Le solide glisse selon la ligne de plus grande pente de ce plan. Le contact solide-plan se fait avec des frottements équivalents à une force unique \(\overrightarrow f \), parallèle à la ligne de plus grande pente du plan et de sens opposée à celui du mouvement.
1. Donner l’énoncé du théorème du centre d'inertie (2ieme loi de Newton). 0.75 pt
2. Faire à l’aide d'un schéma le bilan des forces qui s’exercent sur le solide. 0,5 pt
3. En appliquant le théorème du centre d'inertie au solide (S), déterminer en fonction de \(\alpha \), f, g et m, l'expression de l'accélération du centre d'inertie du solide puis calculer sa valeur numérique 1,75 pt
4. En prenant pour origine des dates, la date où le solide a été lancé, déterminer la loi horaire du mouvement. 1 pt
On donne : m=3kg; f=9N; vO=7 m/s; g=9,8 m/s2 \(\alpha = {60^o}\)
Partie B : Équilibre de deux pendules électrostatiques / 3 points
On considère deux pendules électrostatiques identiques de longueur L, accrochés à un support fixe horizontal en deux points M et N. Ils sont constitués d’un fil isolant de masse négligeable et d‘une boule métallisée assimilable à un point matériel de masse m. On électrise les boules de manière à leur attribuer des charges électriques QA et QB de même valeur absolue Q. À l'équilibre les pendules sont disposés comme l’indique la figure ci-dessous.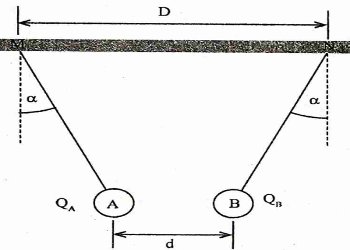
1. Les charges portées par les boules sont-elles de même signe ? Justifier votre réponse. 0,5pt
2. Faire à l'aide d’un schéma, le bilan des forces qui s'exercent sur la boule A. 0,75 pt
En déduire l’expression de l’intensité de la force électrostatique subie par celle-ci en fonction de m, g, \(\alpha \) . 0,75 pt
3. Exprimer alors Q, la valeur absolue commune des charges QA et QB en fonction de m, g, D, L, kC et \(\alpha \) où kC est la constante de Coulomb. On donne kC = 9x10 9N.m2/C-21 pt
Exercice 2 : Les systèmes oscillants / 4 points
Les parties A et B sont indépendantes.
Partie A : Analyse de l Évolution d’un système oscillant à l’oscilloscope / 1,5 point
La grandeur p (t) qui décrit l’évolution temporelle d’un oscillateur est convertie en tension par un dispositif adéquat. La relation entre la tension obtenue et la grandeur caractéristique de l’oscillateur est :
\(u(t) = 0,4p(t)\)
Lorsque celle-ci (la tension obtenue) est injectée dans l’une des voies d’un oscilloscope, on obtient l’oscillogramme de la figure ci-dessous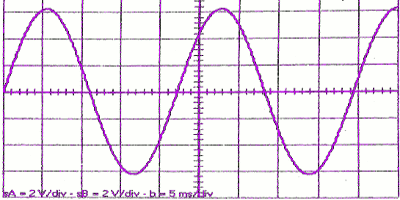
Les réglages de l’oscilloscope sont les suivants : Gain vertical :2 V/div ; Balayage : 5 ms/div.
1. Déterminer l’amplitude et la période de cet oscillateur. 1 pt
2. Écrire une expression de p(t) cohérente avec cet oscillogramme. 0,5 pt
Partie B : Étude d’un pendule simple / 2,5 points
Un pendule est constitué par un solide très dense, de petites dimensions, attaché à une ficelle inextensible de masse négligeable de longueur 80 cm. Le pendule est suspendu à un support fixe. Il est ensuite écarté de sa position d'équilibre d'un angle \(\alpha = {8^o}\), mesuré par rapport à la verticale de son point de suspension et abandonné sans vitesse initiale à une date prise comme origine des dates.
1. Établir l'équation différentielle des oscillations de faible amplitude de ce pendule. On explicitera la démarche mise en œuvre, en particulier en faisant un schéma. 1 pt
2. Exprimer puis calculer la valeur numérique de la période propre de ce pendule. 0.75 pt
3. Écrire la loi horaire de l'évolution temporelle du pendule en utilisant les conditions initiales. 0,75 pt
On prendra g = 9,8 m/s2
Exercice 3 : Phénomènes ondulatoires et corpusculaires/ 5 points
Les parties A et B sont indépendantes.
Partie A: Propagation d ‘une onde le long d'une corde / 2 points
Nous admettrons, avec un choix convenable des conditions initiales, que l'expression de l’élongation d’un point O d'une corde de longueur infinie où se propage une onde transversale a pour expression :
\(y(0,t) = 3\cos (100\pi t)\) (en cm).
La célérité de l'oncle le long de la corde est de 8 m/s.
1. Déterminer la période T de la vibration qui se propage et la longueur d'onde \(\lambda \) de l'onde progressive qui s'établit sur la corde. 1 pt
2. Déterminer l'expression de l'élongation d'un point P de la corde distant de O de 24 cm mesuré dans le sens de la propagation en fonction du temps. 1 pt
Partie B : Radioactivité / 3 points
Un noyau de polonium (Po) est constitué de 84 protons et de 126 neutrons. Ce noyau est radioactif \(\alpha \) et le noyau fils obtenu à l'issue de la transmutation est un noyau de plomb (Pb).
1. Définir : Radioactivité. 0,5pt
2. Déterminer les nombres de masse et de charge du noyau de polonium considéré. 0,5pt
3. Écrire l'équation de la désintégration radioactive de ce noyau de polonium. 1 pt
4. Calculer en MeV l'énergie totale libérée par la désintégration d'un noyau de lpt polonium 210. On donne : mpO = 210,0482 u ; mpb, = 206,0385 u ; mα = 4,0015 u ; 1u = 931,5Mev/c2
Exercice 4 : Mesure de l'intensité de l'accélération de la pesanteur /4 points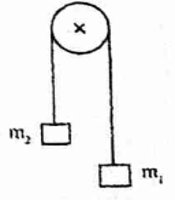
Pour déterminer la valeur de l'intensité de la pesanteur en un lieu, on utilise un dispositif constituée de deux masses m1 et m2 reliées par l'intermédiaire d'un fil passant dans la gorge d'une poulie (Voir figure ci-contre). Lorsque par exemple m1 > m2, la masse m1 effectue un mouvement rectiligne uniformément accéléré. On montre, lorsque \({m_1} \succ {m_2}\), que l'expression l'accélération du centre d'inertie de la masse m1 en fonction g est :
\(a = \frac{{{m_1} - {m_2}}}{{{m_1} + {m_2}}}\)
si on considère que la ficelle est inextensible et que la poulie est de masse négligeable. Pour déterminer une valeur expérimentale de l'accélération de la pesanteur, on réalise pour six hauteurs de chutes, la mesure de la durée de chute. Les données sont présentées dans le tableau ci-dessous :
| h(m) |
0,40 |
0,60 |
0,80 |
1,00 |
1,20 |
1,40 |
1,60 |
| t(s) |
0,65 |
0,80 |
0,92 |
1,03 |
1,13 |
1,22 |
1,31 |
1. Indiquer deux méthodes pour obtenir une valeur expérimentale de l'intensité de la pesanteur au lieu de l'expérience en utilisant les données ci-dessus. 1,5 pt
2. Un groupe d‘élèves a décidé de calculer pour certaines hauteurs de chute, la vitesse moyenne de la bille. Ils obtiennent le tableau de mesures ci-dessous :
| h(m) |
0,40 |
0,60 |
0,80 |
1,00 |
1,20 |
1,40 |
1,60 |
| t(s) |
0,65 |
0,80 |
0,92 |
1,03 |
1,13 |
1,22 |
1,31 |
| \({v_m}(m/s)\) |
|
1,48 |
1,74 |
1,90 |
2,11 |
2,26 |
|
Tracer, en précisant l’échelle choisie, le graphe de \({v_m} = f(t)\). En déduire une valeur de l'accélération de la pesanteur au lieu de l'expérience. 2 pt
3. Commenter la méthode utilisée par ce groupe d'élèves 0,5 pt
On donne : m1 = 576 g ; m2 = 390
CORRECTION
Exercice I Mouvement dans les champs de forces et leurs applications (7 pts)
Partie A : Solide en mouvement sur une piste(4 pts)
1. Énoncé du théorème du centre d’inertie (IIème loi de Newton )
Dans u référentiel galiléen. La somme vectorielle des forces appliquées à un solide est égale au produit de la masse du solide par le vecteur accélération de son centre d’inertie.
2. Bilan des forces à l’aide du schéma
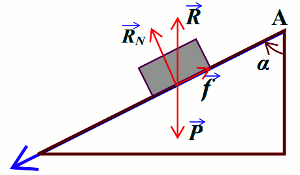Les forces appliquee sur le solide sont :
Son poids \(\overrightarrow P \) et la réaction \(\overrightarrow R \) du plan ( avec pour composantes la force de frottements \(\overrightarrow f \) et la réaction normale du plan incliné \(\overrightarrow {{R_N}} \) )
3. Epression de l’acceleration :
Appliquans le theoreme du centre d’inertie au mobile dans e referentiel terrestre :
\(\sum \overrightarrow {{F_{ext}}} = m.\overrightarrow {{a_G}} \)
Soit \(\overrightarrow R + \overrightarrow P = m.\overrightarrow {{a_G}} \)
En projetant cette relation sur un axe parallèle à la trajectoire et orienté dans le sens du mouvement, on obtient :
\(mg\cos \left( \alpha \right) - f\) \( = m.{a_G}\) soit :
\({a_G} = \) \(g\sin \left( {\frac{\pi }{2} - \alpha } \right)\) \( = 1,9 m.{s^{ - 2}}\)
4. Loi horaire du mouvement.
Le mouvement du solide est rectiligne et uniformément varié
La loi horaire est de la forme :
\(x(t) = \) \(\frac{1}{2}{a_G}{t^2} + {v_A}t + {x_A}\)
Avec \({x_A} = 0\), nous avons :
\(x(t) = 0,95{t^2} + 7t\) en mètres
Partie B : Équilibre de deux pendules électrostatiques (3 pts )
1. Les charges portées par les boules ne sont pas de même signe, car l’interaction électrique est attractive
2. Bilan des forces à l’aide du schéma
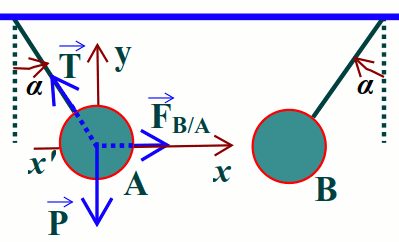- Son poids \(\overrightarrow P \)
- La force électrostatique \({\overrightarrow F _{B/A}}\)
- La tension \(\overrightarrow T \) du fil fixé au point M
Expression de l’intensité de la force électrostatique
A l’équilibre, on a : \(\sum {\overrightarrow F _{ext}} = \overrightarrow 0 \) soit :
\(\overrightarrow P + {\overrightarrow F _{B/A}} + \overrightarrow T = \overrightarrow 0 \)
Par projection dans le repere xAy, on obtient ;
\(\left\{ \begin{array}{l}{F_{B/A}} - T\sin (\alpha ) = 0\\T\cos (\alpha ) - P = 0\end{array} \right.\)
Soit : \({F_{B/A}} = mg\tan (\alpha )\)
3. Expression de Q
Sachant que \({F_{B/A}} = \frac{{k\left| {{Q_A}} \right|\left| {{Q_B}} \right|}}{{{d^2}}}\)
Avec \(d = D - 2L\sin (\alpha )\) on a
\(\frac{{k{Q^2}}}{{{{(D - 2L\sin (\alpha ))}^2}}} = mg\tan (\alpha )\)
Soit :
\(Q = (D - 2L\sin (\alpha ))\sqrt {\frac{{mg\tan (\alpha )}}{k}} \)
Exercice 2 : Systèmes oscillants (4 pts) Partie A : Analyse de l’évolution d’un système oscillant à l’oscilloscope (1,5 pt )
1. Déterminons la période et l’amplitude de cet oscillateur
Amplitude : \({U_m} = 3,2x2 = 6,4V\) et \({P_m} = \frac{{{U_m}}}{{0,4}} = 16V\)
Période : \(T = 4,47x5 = 22,35 ms\)
2. Expression de \(p(t)\)
\(p(t) = {P_m}\cos (\omega t + \varphi )\) avec \(\omega = \frac{{2\pi }}{T}\)
\(p(t) = 16\cos (281t + \varphi )\)
Partie B : Étude d’un pendule simple(2,5 pts)
1. Équation différentielle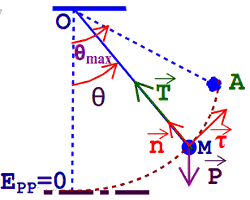
Système : Le solide ponctuel, dans le référentiel terrestre
- Le poids \(\overrightarrow P \) du solide
- La tension \(\overrightarrow T \) du fil
D’après la deuxième loi de Newton \(\sum {\overrightarrow F _{ext}} = m\overrightarrow {{a_G}} \) soit \(\overrightarrow P + \overrightarrow T = m\overrightarrow {{a_G}} \)
En projetant cette relation suivant l’axe (D, \(\overrightarrow \tau \)), avec \(v = L\dot \theta \), nous avons : \(\dot \theta + \frac{g}{L}\theta = 0\)
2. Période des oscillations
\({T_0} = \frac{{2\pi }}{\omega } \Rightarrow \) \({T_0} = 2\pi \sqrt {\frac{L}{g}} \) soit \({T_0} = 1,79 s\)
3. Loi horaire de l’évolution du pendule
Elle est de la forme : \(\theta (t) = {\theta _0}\cos ({\omega _0}t + \varphi )\)
Avec \({\theta _0} = {8^0} \Rightarrow {\theta _0} = \frac{{2\pi }}{{45}}\), \({\omega _0} = \sqrt {\frac{g}{L}} = 3,5rad/s\)
Conditions initiales, à t=0, \(\theta (0) = {\theta _0}\) d’où \(\varphi = 0\)
Finalement
\(\theta (t) = 8\cos (3,5t)\) en degrés
\(\theta (t) = \frac{{2\pi }}{{45}}\cos (3,5t)\) en radians
Exercice 3 : prénommes corpusculaires et ondulatoire (5 pts) Partie A : propagation d’une onde le long d’une corde (2 pts)
1. La période des oscillations
\(T = \frac{{2\pi }}{\omega } = \) \(\frac{{2\pi }}{{100\pi }} = 0,02 s\)
La longueur d’onde des oscillations
\(\lambda = vT = 0,16 m\)
2. Élongation du point P
\(y(P,t) = \) \(3\cos \left( {100\pi t - \frac{{2\pi OP}}{\lambda }} \right)\)
\(y(P,t) = 3\cos \left( {100\pi t - 3\pi } \right)\)
Partie B : La radioactivité(3 pts)
1. La radioactivité est la propriété qu’a un noyau atomique instable de se désintégrer en émettant des particules et en produisant des rayonnements électromagnétiques.
2. Nombre de charge : Z= 84 ; Nombre de masse : A = 126+84 = 210
3. Équation de désintégration
\({}_{84}^{210}Po \to {}_2^4He + {}_Z^APb + E\)
En utilisant les lois de conservation de Soddy, nous avons :
\(\left\{ \begin{array}{l}210 = 4 + A\\84 = 2 + Z\end{array} \right.\) soit \(\left\{ \begin{array}{l}A = 206\\Z = 82\end{array} \right.\)
L’équation devient :
\({}_{84}^{210}Po \to {}_2^4He + {}_{82}^{206}Pb + E\)
4. Calcule de l’énergie libérée
D’après la relation d’Einstein \(E = \left| {\Delta m} \right|{c^2}\), avec \(\left| {\Delta m} \right| = {m_{Po}} - {m_{Pb}} - {m_{He}}\)
\(\left| {\Delta m} \right| = 0,0082u\)
Nous avons :
\(E = 7,64Mev\)
Exercice 4 Mesure de l’intensité de l’accélération de la pesanteur (4 pts) 1. Méthode 1 : Calculer \({t^2}\) pour chaque hauteur, tracer le graphe h=f(t) et déterminer la pente de la droite obtenue puis en déduire g.
Méthode 2 : Calcule de la valeur v de la vitesse pour différentes dates, puis tracer le graphe v=f(t), déterminer la pente de la droite obtenue et en déduire g
2. Tracé de la droite v=f(t)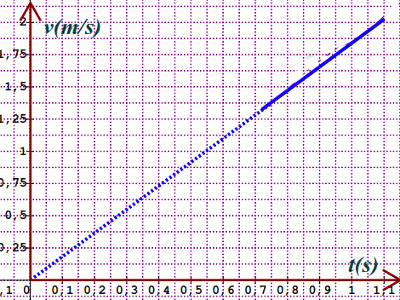
Échelle sur les axes : 1 cm pour 0,1 s et 1 cm pour 0,25 m/s
Valeur de g : de la courbe précédente, nous avons :
\({a_G} = \frac{{\Delta v}}{{\Delta t}} = 1,86m/{s^2}\)
Ainsi : \(g = \frac{{{m_1} + {m_2}}}{{{m_1} - {m_2}}}{a_G} = 9,66 m/{s^2}\)
3. La méthode utilisée par ce groupe d’élèves donne une bonne approximation de la valeur de l’accélération de la pesanteur
Commentaires
Enregistrer un commentaire