TD 2021 MATHEMATIQUES

ENNONCE

Partie A : Évaluation des ressources (15 points)

Cette partie est constituée de trois exercices indépendants numérotés de 1 à 3.

Exercice 1 : (4 points)

On considère la fonction numérique f définie sur $\mathbb{R}$ par : $f(x) = 36{x^2}$ $- 2{x^3}$
1. Montrer que $f$ est une solution sur $\mathbb{R}$ de l'équation différentielle (E) :
$36y'' + 6y'$ $+ y = 2592$ $- 2{x^3}$ 1pt
2. Étudier les variations de la fonction f sur l'intervalle [0,18] et déterminer la valeur de $x$ pour laquelle f atteint son maximum sur cet intervalle. 1,5pt
3. Une région reçoit 36 doses de vaccin à la COVID -19 dont $n$ doses proviennent d'une firme A, $n$ doses proviennent d'une firme B et le reste d'une firme C (avec $1 \le n \le 17$).
On tire au hasard et simultanément 3 doses de vaccin du lot.
a) Démontrer que le nombre de tirages donnant une dose de chaque firme est $f(n)$.0,5pt
b) Soit P(n) la probabilité de tirer une dose de chaque firme. Exprimer $P(n)$ à l'aide de
$f(n)$ et en déduire la valeur de $n$ pour laquelle $P(n)$ est maximale. 1pt

Exercice 2 : (5 points)

Le plan est muni d'un repère orthonormé $\left( {O,I,J} \right)$. On considère dans $\mathbb{C}$ l'équation :
$\left( E \right):{z^3} -$ $\left( {6 + i\sqrt 3 } \right){z^2} +$ $\left( {11 + 4i\sqrt 3 } \right)z$ $- 6 - 3i\sqrt 3 = 0$
1. Montrer que l'équation $\left( E \right) \Leftrightarrow$ $\left( {{z^2} - 4z + 3} \right)$ $\left( {z - 2 - i\sqrt 3 } \right)$ $= 0$ 0,5pt
2. Résoudre dans $\mathbb{C}$ l'équation (E). 0,75 pt
3. On considère les points A, B, C et D d’affixes respectives 3, $2 + i\sqrt 3$ , 7 et $11 + 4i\sqrt 3$
a) Démontrer que le triangle IAB est équilatéral. 0.5pt
b) Soit $r$ la rotation de centre le point F et d'angle $\frac{\pi }{3}$; d'écriture complexe :
$z' = \left( {\frac{1}{2} + i\frac{{\sqrt 3 }}{2}} \right)z$ $+ \frac{3}{2} + 2\sqrt 3 +$ $\left( {2 - \frac{{3\sqrt 3 }}{2}} \right)i$.
Déterminer l’affixe du point F et montrer que $r\left( C \right) = D$, en déduire alors que le triangle DFC est équilatéral. 1,5pt
c) Déterminer l'écriture complexe de l'homothétie h qui transforme I en D et B en C. 1pt
d) Déterminer l'expression complexe de la transformation $S = h^\circ r$. 0,75 pt

Exercice 3 (4,25 points)

On définit les fonctions $h$ et $h$ sur $\left] {0, + \infty } \right[$ par: $f(x) = {e^{\frac{{x + 1}}{x}}}$ et $k(x) = - x$ $+ x\ln x$
1. Démontrer que l'équation $k(x) = 1$ admet une unique solution $\alpha$ dans $\left[ {3;4} \right]$. 1pt
2. Démontrer que $k(x) = 1$ si et seulement si $h(x) = x$. 0,25 pt
3. Démontrer que pour tout x élément de $\left[ {3;4} \right]$ , $h(x)$ est aussi un élément de $\left[ {3;4} \right]$. 0,5pt
4. Démontrer que $\left| {h'(x)} \right| \le \frac{1}{2}$ à pour tout x élément de $\left[ {3;4} \right]$. 0,5pt
5. Soit U la suite définie par : $\left\{ \begin{array}{l}{U_0} = 3\\{U_{n + 1}} = h({U_n})\end{array} \right.$, avec $n \in \mathbb{N}$
a) Démontrer par récurrence que pour tout entier naturel $n$. ${U_n} \in \left[ {3;4} \right]$. 0.5pt
b) Démontrer que pour tout entier naturel $n$. $\left| {{U_{n + 1}} - \alpha } \right|$ $\le \frac{1}{2}\left| {{U_n} - \alpha } \right|$ 0 ,5pt
c) En déduire que pour tout entier naturel $n$ , $\left| {{U_n} - \alpha } \right| \le$ ${\left( {\frac{1}{2}} \right)^n}$ 0,5pt
d) Démontrer que la suite U est convergente et déterminer sa limite. 0,5pt

Partie B : Évaluation des compétences (6,75 points)

Situation :
Une réserve naturelle contient essentiellement trois espèces de singes : des macaques ; des orang-outans et des chimpanzés. Les relevés topographiques de cette réserve naturelle simulés dans un laboratoire montrent que celle-ci est limitée dans un repère orthonormé $\left( {O,I,J} \right)$ à l'échelle 1cm pour 4km, par la courbe (C) d'équation $y = {x^3} -$ $3{x^2} + 4$, la droite $\left( {OI} \right)$ et les droites $\left( {{D_1}} \right)$ et $\left( {{D_2}} \right)$ d'équations respectives $x = - 1$ et $x = 2$.
Deux routes rectilignes assimilées aux droites $\left( {OJ} \right)$ et $\left( {D} \right)$ d'équation $x = 1$ divisent la réserve en trois sites distincts :
♦ Le site A contenant des macaques est délimité par la courbe (C), les droites $\left( {OI} \right)$, $\left( {{D_1}} \right)$ et $\left( {OJ} \right)$
♦ Le site B contenant des orang-outans est délimité par la courbe (C), les droites $\left( {OI} \right)$, $\left( {OJ} \right)$ et $\left( {D} \right)$.
 Le site C contenant des chimpanzés est délimité par la courbe (C), les droites $\left( {OI} \right)$, $\left( {D} \right)$ et $\left( {{D_2}} \right)$.
La densité de la population de macaques est de 15 macaques par km’, celle d'orang-outans est de 10 orang-outans par km2 et celle des chimpanzés est de 12 chimpanzés par km2. Pour protéger certains animaux de la réserve contre les zoonoses (maladies des bêtes), les chercheurs les vaccinent 3 fois. La première vaccination nécessite 1 ,136 litre de vaccin. La deuxième nécessite 1,54 litre. Les doses de vaccin (en millilitres) par animal sont données par le tableau suivant :

	macaque	orang-outan	chimpanzé
1ère dose de vaccin	2 ml	1 ml	3 ml
2ème dose de vaccin	2 ml	3 ml	4 ml
3ème dose de vaccin	2 ml	5 ml	5 ml

Dans la réserve. 15% de chimpanzés ont une maladie ${M_1}$. Parmi les chimpanzés atteints par la maladie ${M_1}$, 20% ont une maladie ${M_2}$ et parmi les chimpanzés non atteints par la maladie ${M_1}$, 4% ont la maladie ${M_2}$. On choisit un chimpanzé au hasard pour une étude dans un laboratoire.

Tâches :
1. Déterminer le nombre d'animaux de cette réserve. 2,25 pts
2. Déterminer le volume de vaccin en litres nécessaire pour la 3eme vaccination. 2,25 pts
3. Déterminer la probabilité pour que le chimpanzé choisi soit atteint de la maladie ${M_2}$. 2,25pts

CORRECTION

Partie A : Évaluations des ressources / 15 points

Exercice 1 / 4 points

1. On donne la fonction $f$ définie sur $\mathbb{R}$ par $f(x) = 36{x^2}$ $- 2{x^3}$
Montrons que $f$ est une solution sur $\mathbb{R}$ de l'équation différentielle
$\left( E \right):36y'' +$ $6y' + y =$ $2592 - 2{x^3}$
Nous avons $\left\{ \begin{array}{l}f(x) = 36{x^2} - 2{x^3}\\f'(x) = 72x - 6{x^2}\\f''(x) = 72 - 12x\end{array} \right.$
Pour tout $x \in \mathbb{R}$, on a : $36f''(x) +$ $6f'(x) + f(x)$ $= 2592 - 2{x^3}$, $f$ est donc une solution de l'équation différentielle $\left( E \right)$. 1 pt
2. Etudions les variations de f sur l'intervalle $\left[ {0;18} \right]$ et déterminons la valeur de $x$ pour laquelle $f$ atteint son maximum 1,5 pt
On a : $f'(x) = 72x$ $- 6{x^2} =$ $6x(12 - x)$ et $f'(x) = 0$ $\Rightarrow 6x(12 - x)$ $= 0 \Rightarrow$ $\left\{ \begin{array}{l}x = 0\\x = 12\end{array} \right.$
D'où le tableau :
$f$ est strictement croissante sur $\left[ {0;12} \right]$ et strictement décroissante sur $\left[ {12;18} \right]$, alors $f(12)$ est le maximum $f$ sur $\left[ {0;18} \right]$.
La fonction $f$ atteint donc sur $\left[ {0;18} \right]$ le maximum en $x = 12$.
3-a) Démontrons que le nombre de tirages donnant une dose de chaque firme est $f(n)$
On choisit une dose par firme A, B et C. Ces firmes ayant respectivement n , n et $36 - 2n$ dose. Le tirage étant simultané, le nombre de tirages possibles donnant une dose de chaque firme est : 0,5 pt
$C_n^1 \times C_n^1 \times$ $C_{36n - 2n}^1 =$ ${n^2}\left( {36 - 2n} \right)$ $= f(n)$
3.b) Donnons l'expression de $P(n)$ en fonction de $f(n)$ et déterminons la valeur de $n$ pour laquelle $P(n)$ est maximale 1 pt
$P(n)$ est la probabilité de tirer une dose de chaque firme.
$P(n) =$ $\frac{{C_n^1 \times C_n^1 \times C_{36n - 2n}^1}}{{C_{36}^3}}$ $= \frac{{f(n)}}{{7140}}$
La valeur de $n$ qui rend $P(n)$ maximale est la même que celle qui rend $f(n)$ maximale. Et d'après la question 2, une telle valeur de $n$ est 12.

Exercice 2

$\left( {O;I,J} \right)$ est un repère orthonormé du plan. On considère dans $\mathbb{C}$ l'équation
$\left( E \right):{z^3} -$ $\left( {6 + i\sqrt 3 } \right){z^2} +$ $\left( {11 + 4i\sqrt 3 } \right)z$ $- 6 - 3i\sqrt 3 = 0$
1- Montrons que l'équation $\left( E \right) \Leftrightarrow$ $\left( {{z^2} - 4z + 3} \right)$ $\left( {z - 2 - i\sqrt 3 } \right)$ $= 0$
En développant l’expression précédente, nous obtenons $\left( E \right)$. D'où l’équivalence attendue. 0,5 pt
2. Résolvons dans c l'équation (E) 0,75 pt
$\left( E \right) \Leftrightarrow$ $\left( {{z^2} - 4z + 3} \right)$ $\left( {z - 2 - i\sqrt 3 } \right)$ $= 0 \Rightarrow$ $\left\{ \begin{array}{l}{z^2} - 4z + 3 = 0\\z = 2 + i\sqrt 3 \end{array} \right.$
L'ensemble solution de l'équation $\left( E \right)$ est donc $\left\{ {1,3,2 + i\sqrt 3 } \right\}$.
3.a) On donne les points A, B, C et D d’affixes respectives ${{z_A} = 3}$, ${z_B} = 2 + i\sqrt 3 , \({{z_C} = 1}$ et ${z_D} = 11 + 4i\sqrt 3$
3) Démontrons me le triangle IAB est équilatéral 0,5 pt
3-a) Première approche:
$IA =$ $\left| {{z_A} - {z_I}} \right| = 2$
$IB =$ $\left| {{z_B} - {z_I}} \right|$ $= \left| {1 + i\sqrt 3 } \right|$ $= 2$
$AB =$ $\left| {{z_B} - {z_A}} \right| =$ $\left| { - 1 + i\sqrt 3 } \right| = 2$
D'où $AI = IB$ $= AB$
IAB est donc un triangle équilatéral.
Deuxieme approche : On a : $\frac{{{z_B} - {z_I}}}{{{z_A} - {z_I}}} =$ $\frac{{1 + i\sqrt 3 }}{2}$ $= {e^{i\frac{\pi }{3}}}$. De cette relation, on a $AI = IB$ et$mes\left( {\widehat {\overrightarrow {IA} ,I\overrightarrow B }} \right)$ $= {60^o}$, IAB est donc un triangle équilatéral.
3.b) Déterminons l’affixe du point $F$ centre de la rotation et montrons que $r(C) = D$ 1,5 pt
La rotation $r$ a pour expression complexe $z' = \left( {\frac{1}{2} + i\frac{{\sqrt 3 }}{2}} \right)z$ $+ 2\sqrt 3 + \frac{3}{2} +$ $\left( {2 - \frac{{3\sqrt 3 }}{2}} \right)i$
comme $F$ est le centre de$r$, on a $r(F) = F$.
D'où ${z_F} = 3 + 4i$
On pourra remarquer à travers des calculs que $r(C) \ne D$
3.c) Donnons l'expression complexe de l’homothétie $h$ telle $h(I) = D$ et $h(B) = C$
L’homothétie $h$ a pour expression complexe : $z' = a + ib$ avec $a \in \mathbb{R}$.
$h(I) = D$ $\Leftrightarrow az + b$ $= 11 + 4i\sqrt 3$ et $a\left( {2 + i\sqrt 3 } \right)$ $+ b = 7$. Ce qui donne $a = - 4$ et $b = 15 + 4i\sqrt 3$ soit $z' = - 4z +$ $15 + 4i\sqrt 3$ est l'expression complexe de $h$.
3.d) Déterminons l'expression complexe de $s = h^\circ r$
$r$ a pour expression complexe $z' = \left( {\frac{1}{2} + i\frac{{\sqrt 3 }}{2}} \right)z$ $+ 2\sqrt 3 + \frac{3}{2} +$ $\left( {2 - \frac{{3\sqrt 3 }}{2}} \right)i$ et celle de $h$ est $z' = - 4z +$ $15 + 4i\sqrt 3$ ; Celle de $s = h^\circ r$ est donc
$z' = - 4|$ $\left( {\frac{1}{2} + i\frac{{\sqrt 3 }}{2}} \right)z +$ $2\sqrt 3 + \frac{3}{2} +$ $\left( {2 - \frac{{3\sqrt 3 }}{2}} \right)i| +$ $15 + 4i\sqrt 3 =$ $\left( { - 2 - 2i\sqrt 3 } \right)z$ $+ 9 - 8\sqrt 3 + i$ $\left( { - 8 + 10\sqrt 3 } \right)$ 0,75 pt

Exercice 3

on donne $h(x) = {e^{\frac{{x + 1}}{x}}}$ et $k(x) = - x +$ $x\ln x$ définies sur $\left] {0, + \infty } \right[$
1. Démontrons que l'équation $k(x) = 1$ admet une unique solution $a \in \left[ {3,4} \right]$ 1 pt
la fonction $k$ est dérivable sur $\left] {0, + \infty } \right[$ et $k'(x) = \ln x$.
D'où $k'(x) \succ 0$ pour $x$ appartenant à l'intervalle $\left[ {3,4} \right]$.
$k$ est continue et strictement croissante sur $\left[ {3,4} \right]$ avec 1 appartenant à
$1 \in k\left( {\left[ {3,4} \right]} \right)$ $= \left[ {k(3),k(4)} \right]$ $= [ - 3 + 3\ln 3,$ $- 4 + 4\ln 4]$, puisque -$- 3 + 3\ln 3 = 0,29..$ et $- 4 + 4\ln 4$ $= 1,54...$.
L'équation $k(x) = 1$ admet alors une unique solution $a$ appartenant à l'intervalle $\left[ {3,4} \right]$..
2. Démontrons que $k(x) = 1$ si et seulement si $h(x) = x$
Soit $x \succ 0$, on a: $k(x) = 1 \Leftrightarrow$ $- x + x\ln x$ $= 1 \Rightarrow \ln x$ $= \frac{{x + 1}}{x}$
$\Rightarrow x = {e^{\frac{{x + 1}}{x}}}$ $\Leftrightarrow h(x) = x$ 0,25 pt
Démontrons que si $x \in \left[ {3,4} \right]$, alors $h(x) \in \left[ {3,4} \right]$ 0,5 pt
Soit $x \in \left[ {3,4} \right]$, $h$ est une fonction dérivable sur $\left[ {3,4} \right]$ et $h'(x) = - \frac{1}{{{x^2}}}{e^{\frac{{x + 1}}{x}}}$ $\prec 0$. $h$ est donc strictement décroissante sur $\left[ {3,4} \right]$
De $3 \le x \le 4$, on a $h(4) \le h(x)$ $\le h(3) \Rightarrow$ $3,49 \le h(x)$ $\le 3,80$ ainsi $3 \le h(x) \le 4$
3. Démontrons que $\left| {h(x)} \right| \le \frac{1}{2}$ pour tout $x \in \left[ {3,4} \right]$
On a $h'(x) = -$ $\frac{1}{{{x^2}}}h(x)$ et donc $\left| {h'(x)} \right| =$ $\frac{1}{{{x^2}}}h(x)$
$3 \le x \le 4$ $\Rightarrow \frac{1}{{16}} \le \frac{1}{{{x^2}}}$ $\le \frac{1}{9}$ et $3 \le h(x) \le 4$ soit $\frac{3}{{16}} \le \frac{1}{{{x^2}}}h(x)$ $\le \frac{4}{9}$
$\frac{3}{{16}} \le \left| {h'(x)} \right|$ $\le \frac{4}{9}$ ainsi $\left| {h'(x)} \right| \le \frac{1}{2}$ car $\frac{4}{9} \le \frac{1}{2}$ 0,5 pt
5. On donne la suite $U$ définie par ${u_0} = 3$ et ${u_{n + 1}} = f({u_n})$ 0,5 pt
5.a) Démontrons que pour tout $n \in \mathbb{N}$, ${u_n} \in \left[ {3,4} \right]$
Procédons par récurrence.
Au rang $n = 0$, on a ${u_0} = 3$ appartenant à $\left[ {3,4} \right]$.
Soit $n \in \mathbb{N}$, Supposons que ${u_n} \in \left[ {3,4} \right]$. On a d'après la question 3, on a $h({u_n}) \in \left[ {3,4} \right]$. D'où ${u_{n + 1}} \in \left[ {3,4} \right]$
Conclusion : Pour tout $n \in \mathbb{N}$, ${u_n} \in \left[ {3,4} \right]$
5.b) Démontrons que pour tout $n \in \mathbb{N}$, $\left| {{u_{n + 1}} - a} \right| \le$ $\frac{1}{2}\left| {{u_n} - a} \right|$
Pour tout $n \in \mathbb{N}$, ${u_n} \in \left[ {3,4} \right]$, et $\left| {h'(x)} \right| \le \frac{1}{2}$, pour $x$ appurtenant à $\left[ {3,4} \right]$.
Des Inégalités des Accroissements Finis, on a $\left| {h({u_{n + 1}}) - h(a)} \right|$ $\le \frac{1}{2}\left| {{u_n} - a} \right|$ . Or ${u_{n + 1}} = h({u_n})$ et $h(a) = a$ car $h(a) = 1$ donc $\left| {{u_{n + 1}} - a} \right| \le$ $\frac{1}{2}\left| {{u_n} - a} \right|$
5.c) Déduisons-en que pour tout $n \in \mathbb{N}$, $\left| {{u_n} - a} \right| \le {\left( {\frac{1}{2}} \right)^n}$
Procédons par récurrence.
Au rang $n = 0$, on a $\left| {{u_{n + 1}} - a} \right| =$ $\left| {{u_0} - a} \right| =$ $\left| {3 - a} \right| \le \left| {3 - 4} \right|$ car $a \in \left[ {3,4} \right]$
D’où $\left| {{u_{n + 1}} - a} \right|$ $\le {\left( {\frac{1}{2}} \right)^n}$ pour $n = 0$
Soit $n \in \mathbb{N}$, Supposons que $\left| {{u_n} - a} \right| \le {\left( {\frac{1}{2}} \right)^n}$
D’apres la question 5.b) on a $\left| {{u_{n + 1}} - a} \right| \le$ $\frac{1}{2}\left| {{u_n} - a} \right|$ ce qui entraine $\left| {{u_{n + 1}} - a} \right| \le$ $\frac{1}{2}{\left( {\frac{1}{2}} \right)^n} \le$ ${\left( {\frac{1}{2}} \right)^{n + 1}}$ d’où $\left| {{u_n} - a} \right| \le {\left( {\frac{1}{2}} \right)^n}$ 0,5 pt
5.d ) Démontrons que la suite $u$ est convergente et déterminons sa limite
On a $\left| {{u_n} - a} \right| \le {\left( {\frac{1}{2}} \right)^n}$ où la suite ${\left( {\frac{1}{2}} \right)^{n + 1}}$ converge vers 0; Par la propriété d'encadrement, on en déduit que ${\left( {{u_n}} \right)}$ converge vers a.

Partie B : Évaluation des compétences

Solutions
Déterminons les nombre d’animaux de cette réserve
On procèdera par les étapes suivantes :
n On étudie les variations de la fonction g définie sur $\left[ { - 1; + \infty } \right[$ par : $g(x) = {x^3} -$ $3{x^2} + 4$. La fonction $g$ est une fonction polynôme, elle est donc dérivable sur $\mathbb{R}$. Sa dérivée est $g'(x) = 3{x^2}$ $- 6x = 3x$ $\left( {x - 2} \right)$. Les solutions de
l'équation $g'(x) = 0$ $\Leftrightarrow \left\{ \begin{array}{l}x = 0\\x = 2\end{array} \right.$. Le tableau de variation de g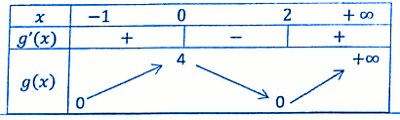
On construit la courbe représentative (C) de g pour identifier les aires
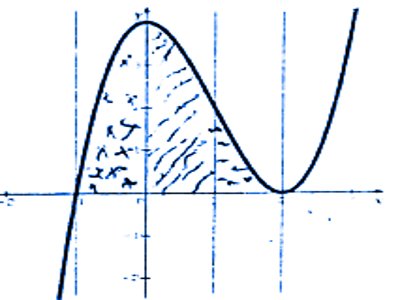Calculons les aires ${A_1}$,. ${A_2}$ et ${A_3}$ occupées respectivement par les macaques, les orang -outans et des chimpanzés en unités d’aires
${A_1} = \int_{ - 1}^0 {g(x)dx}$ $= \left[ {\frac{1}{4}x4 - x3 + 4x} \right]_{ - 1}^0$ $= \frac{{11}}{4}$, donc ${A_1} = 44$ km2
${A_2} = \int_{ 0}^1 {g(x)dx}$ $= \left[ {\frac{1}{4}x4 - x3 + 4x} \right]_{ 0}^1$ $= \frac{{13}}{4}$, donc ${A_2} = 52$ km2
${A_3} = \int_{ 1}^2 {g(x)dx}$ $= \left[ {\frac{1}{4}x4 - x3 + 4x} \right]_{ 1}^2$ $= \frac{{3}}{4}$, donc ${A_3} = 12$ km2
On calcule le nombre d'animaux de la réserve en fonction des aires Le nombre de macaques est : ${N_1} = 15 \times 44$ $= 660$
Le nombre des orangs- outangs est: ${N_2} = 10 \times 52$ $= 520$
Le nombre de chimpanzés est de : ${N_3} = 12 \times 12$ $= 144$
Le nombre total d'animaux de la réserve est donc ${N_1} + {N_2} +$ ${N_3} = 1324$
Déterminons le volume de vaccin nécessaire pour la troisième vaccination
Soient x, y et z le nombre respectif de macaques, des orangs outans et des chimpanzés qui doivent être vaccinés et soit D la troisième dose administrée aux animaux.
La première dose est traduite par la relation $2x + y +$ $3z = 1136$, ${E_1}$
La deuxième dose est traduite par la relation : $2x + 3y +$ $4z = 1540$, ${E_2}$
La troisième dose est traduite par la relation : $2x + 5y +$ $5z = D$, ${E_3}$
En effectuant la différence ${E_1} - {E_2}$, on obtient la relation : $2y + z = 404$
En effectuant la différence ${E_3} - {E_2}$, on obtient la relation : $2y + z =$ $D - 1540$
De ces deux dernières relations, $D = 1944$. La dose cherchée est donc $D = 1,944$ L
Déterminons la probabilité pour que le chimpanzé choisi soit atteint de la maladie ${M_2}$
On note $\overline {{M_1}}$ l'évènement : ne pas avoir la maladie ${{M_1}}$. Les probabilités sonnées sont les suivantes :
$p\left( {{M_1}} \right) = \frac{{15}}{{100}}$
$p\left( {{M_2}/{M_1}} \right) = \frac{{20}}{{100}}$
$p\left( {{M_2}/\overline {{M_1}} } \right) = \frac{4}{{100}}$
${M_2} =$ $\left( {{M_1} \cap {M_2}} \right) \cup$ $\left( {\overline {{M_1}} \cap {M_2}} \right)$ ou $\left( {\overline {{M_1}} \cap {M_2}} \right)$ et $\left( {{M_1} \cap {M_2}} \right)$ sont disjoints
On a la probabilité $p\left( {{M_2}} \right) =$ $p\left( {{M_1} \cap {M_2}} \right)$ $+ p\left( {\overline {{M_1}} \cap {M_2}} \right)$
$p\left( {{M_2}} \right) = \frac{{20}}{{100}} \times$ $\frac{{15}}{{100}} + \frac{4}{{100}} \times$ $\frac{{85}}{{100}} = \frac{{640}}{{10000}}$ $= 0,064$