TC/TD 2018 CHIMIE

ENNONCE

Exercice 1 : chimie organique /6 points.
1-Un alcène A a pour formule brute ${C_n}{H_{2n}}$. Son hydratation en présence de l'acide sulfurique conduit a un compose B.
1-1- Écrire l'équation-bilan de la réaction et préciser la fonction de B. 0,75 pt
1-2- Sachant que B renferme en masse 21,6% d'oxygène, déterminer sa formule brute. 0,5 pt
1-3 Écrire les différentes formules semi-développées possibles de B. 0,5 pt
1-4- L'oxydation ménagés de B étant impossible, déduire les formules semi-développées de A et B 0.5pt
2-Une amine tertiaire A de formule ${C_3}{H_9}N$ réagit avec le 1-iodobutane en solution dans l'éther. Il se forme Un précipité blanc.
2-1- Écrire l'équation- bilan de la réaction en utilisant les formules semi-développées. 0,5pt
2-2- Nommer le produit formé. 0,5pt
2-3- Identifier le caractère de l’amine, mis en évidence dans cette réaction. 0,25pt
3- On considère un acide $\alpha$- aminé de masse molaire M = 131 g/mol dont le groupe R est un radical alkyle saturé à une seule ramification
3-1-Ecrire la formule générale des acides $\alpha$- aminés. 0,5pt
3-2- Déterminer sa formule brute 0,5pt
3-3 Sachant que la molécule d'acide $\alpha$-aminé ne comporte qu'un seul atome de carbone asymétrique, en déduire sa formule semi- développée et préciser son nom en nomenclature systématique. 1pt
Masses molaires atomiques en g/mol : C = 12 ; H =1 ; 0 = 16.

EXERCICE 2 : ACIDES-BASES I 6 points ,
l- Définir un acide faible. 0,5pt
2- Deux solutions aqueuses à 25°C ont un pH identique de valeur 3,4.
La première est une solution d'acide chlorhydrique $\left( {{H_3}{O^ + } + C{l^ - }} \right)$ de concentration ${C_1} = 4,0 \times {10^{ - 2}}$ mol/L.
La deuxième est une solution d'acide éthanoïque $C{H_3}COOH$ de concentration ${C_2} = {10^{ - 2}}$ mol/L.
2-1- Calculer la concentration des ions hydronium ${{H_3}{O^ + }}$ dans ces solutions 0,5pt
2-2- Montrer que l'acide éthanoïque est un acide faible 0,5pt
2-3- Écrire l'équation-bilan de la réaction entre l'acide éthanoïque et l'eau. 0,5pt
2-4- Calculer les concentrations des différentes espèces chimiques présentes dans la solution d'acide éthanoïque.
En déduire le pKa de l'acide éthanoïque. 1,5 pt
3-On réalise le dosage d'un volume $Va = 50$ ml d'un acide carboxylique de formule ${C_n}{H_{2n}}{O_2}$ par une solution d'hydroxyde de sodium. Pour atteindre le point d'équivalence, on doit verser un volume $Vb = 100$ ml de solution d'hydroxyde de sodium de concentration $Cb = 0,100$ mol/L
3-1- Déterminer la concentration molaire $Ca$ de la solution d'acide carboxylique. 0,75 pt
3-2- Cette solution est obtenue en dissolvant m = 20,4 g d'acide carboxylique dans V = 1 L d'eau; en d&eacueacute;duire la masse molaire de cet acide. 1pt
3-3- Déterminer sa formule brute. 0,5pt
Masses molaires atomiques en g/mol : C = 12 ; H =1 ; 0 = 16.

Exercice 3 : chimie générale / 4points
1-Niveau d'énergie / 2 points
Les niveaux d'énergie de l’atome d’hydrogène sont donnés par la relation ${E_n} = - \frac{{13,6}}{{{n^2}}}$ (eV).
1-1- Définir énergie d'ionisation. 0,5pt
1-2- Pris dans son état fondamental, l'atome d'hydrogène est excité et son électron passe du niveau 1 au niveau p > 1.
1-2-1- Y-a-t-il absorption ou émission des photons? Justifier votre réponse. 0,5pt
1-2-2 Établir l'expression littérale de la fréquence des radiations émises lorsque cet atome passe d'un état excité p à l'état n = 1. 0,5pt
1-2-3- Calculer cette fréquence pour p = 3. 0,5pt
Données : 1ev = $1,6 \times {10^{ - 19}}$J Constante de Planck h = $6,62 \times {10^{ - 34}}$ J.s
2- Cinétique chimique /2 points
On étudie la cinétique de la réaction d'oxydation des ions iodure ${I^ - }$ en milieu acide par l'eau oxygénée ${H_2}{O_2}$ de concentration ${C_1} = 4,5 \times {10^{ - 2}}$ mol/L Cette réaction lente a pour équation-bilan :
${H_2}{O_2} +$ $2{I^ - } +$ $2{H_3}{O^ + }$ $\to {I_2}$ $+ 4{H_2}O$
À l'instant t = 0 min, On mélange dans un bécher 100 mL de la solution ${S_1}$ d'eau oxygénée et 100 mL d'une solution d’iodure de potassium $({K^ + } + {I^ - })$ de concentration ${C_2} = 2,0 \times {10^{ - 1}}$ mol/L.
On y ajoute quelques gouttes d'acide sulfurique. La solution obtenue est repartie dans 10 béchers à raison de 20 mL par bécher. À L'instant t = 3 min, on ajoute rapidement de la glace dans le premier bécher et on dose le diiode formé par une solution de thiosulfate de sodium $(2N_a^ + + {S_2}O_3^{2 - })$ de concentration $C'$ en présence de l'empois d'amidon. Soit $V'$ le volume de la solution de thiosulfate versé à l'équivalence.
Toutes les trois minutes, on renouvelle l'opération ci-dessus sur le 2ieme puis le 3ieme, etc. La réaction du dosage est rapide et totale. Son équation-bilan est :
${I_2} +$ $2{S_2}O_3^{2 - }$ $\to 2{I^ - }$ $+ {S_4}O_6^{2 - }$
2-1- Montrer que dans le mélange du départ, les ions iodure sont en excès. 0,5 pt
2-2 Pourquoi ajouter-t-on de la glace rapidement à l’ instant t à chaque bécher? 0,5pt
2-3 Montrer que la concentration du diiode apparu dans un bécher à l'instant t a pour expression: ${\left[ {{I_2}} \right]_t} = \frac{1}{2}C'\frac{{V'}}{V}$
où V est le volume de diiode présent dans le bécher. 0,5pt
2-4 Calculer la valeur de la concentration ${\left[ {{I_2}} \right]_t}$, en diiode à la fin de la réaction. 0,5pt

Exercice 4: A caractère expérimental /4 points
1- Préparation d'une solution
On veut préparer V = 250 mL d'une solution d'acide chlorhydrique S de concentration C = ${10^{ - 1}}$mol/L, à partir d'une solution S, disponible. Sur la paillasse du laboratoire, on trouve le matériel et les produits suivants :
Matériel :
Une burette graduée de 50 mL;
Deux béchers de 150ml. et 500 mL ;
Deux fioles jaugées de 250 mL et 500 mL;
Pipettes jaugées de 10 mL et 20 mL.
Produits :
Une solution d'acide chlorhydrique ${S_o}$ de concentration $Co = 2,5$mol/L ;
Une solution ${S_1}$ d'hydroxyde de sodium de concentration ${C_1} = {10^{ - 1}}$ mol/L et de l'eau distillée.
1-1 Calculer le volume de la solution ${S_o}$ a prélever pour cette préparation 0,5 pt
1-2 Citer deux éléments du matériel nécessaire pour la préparation de la solution S 0,5 pt
1-3 Décrire brièvement le mode opératoire pour cette préparation. 0,5 pt
2. Vérification de la concentration
Pour vérifier la concentration de la solution S, on prélève Va = 20 mL de celle-ci que l'on introduit dans le bécher de 100 mL. À l'aide de la burette, on y verse progressivement la solution d'hydroxyde de sodium ${S_1}$. Un pH- mètre permet de suivre l'évolution du pH du mélange pendant le dosage.
Le tableau suivant indique les valeurs de pH obtenues pour différentes valeurs de volume $Vb$, d'hydroxyde de sodium versé :

Vb(mL)	0	5	7	10	12	15	16	17	18	19	20	21	22
pH	1	1,1	1,2	1,3	1,5	1,8	2,0	2,2	2,3	3	9	11,2	11,7

2-1 Construire la courbe $pH = f(Vb)$ sur le papier millimétré à remettre avec la copie.
Échelle: 1 cm pour 1 mL et 1 cm pour une unité de pH. 1pt
2-2 Déduire de la courbe, le volume $Vb$ d'hydroxyde de sodium versé à l'équivalence. 0,5pt
2-3 Calculer la concentration $Ca$ de la solution S. 0,5 pt
2-4 Comparer la valeur Ca obtenue à C et en déduire le rôle du dosage. 0,5 pt

CORRECTION

Exercice 1 : Chimie organique /6pts
1.1 Équation bilan de la réaction
${C_n}{H_{2n}} +$ ${H_2}O$ $\overbrace \to ^{{H_2}S{O_4}}$ $\:{C_n}{H_{2n + 2}}O$(0,5 pt)
La fonction de B : C’est un alcool (0,25 pt)
1.2 Formule brute de B
$\% O = \frac{{1600}}{{14n + 18}}$ $= 21,6$ $\Rightarrow n = 4$(0,25 pt)
B est dont de formule brute : ${C_4}{H_{10}}O$
1.3 Les formules semi-développés possibles de B (0,25x4=1pt)
a) ${H_3}C -$ $C{H_2} -$ $C{H_2} -$ $C{H_2}OH$
b) $\begin{array}{*{20}{c}}{{H_3}C - }&{CH}&{ - C{H_2}OH}\\{}&|&{}\\{}&{C{H_3}}&{}\end{array}$
c) $\begin{array}{*{20}{c}}{{H_3}C - }&{CH}&{ - C{H_2} - CH3}\\{}&|&{}\\{}&{OH}&{}\end{array}$
d) $\begin{array}{*{20}{c}}{}&{C{H_3}}&{}\\{}&|&{}\\{{H_3}C - }&{C - }&{C{H_3}}\\{}&|&{}\\{}&{OH}&{}\end{array}$
1.3 Formules semi-développées de A et B (0,25x2=0,5 pt)
A : $\begin{array}{*{20}{c}}{{H_3}C - }&C&{ = C{H_2}}\\{}&|&{}\\{}&{C{H_3}}&{}\end{array}$
B : $\begin{array}{*{20}{c}}{}&{C{H_3}}&{}\\{}&|&{}\\{{H_3}C - }&C&{ - C{H_3}}\\{}&|&{}\\{}&{C{H_3}}&{}\end{array}$
2.1 Équation-bilan de la réaction
$\begin{array}{*{20}{c}}{{H_3}C - }&{\bar N}&{C{H_3}}\\{}&|&{}\\{}&{C{H_3}}&{}\end{array}$ $+ {H_3}C - C{H_2}$ $- C{H_2} - I$ $\to$ $\begin{array}{*{20}{c}}{}&{C{H_3}}&{}\\{}&|&{}\\{{H_3}C - }&{{N^ + }}&{ - C{H_3}}\\{}&|&{}\\{}&{{{(C{H_2})}_3} - C{H_3}}&{}\end{array}$ $+ {I^ - }$ (0,5pt)
2.2 Nom du produit formé : Iodure de butyltriméthylammonium. (0,5 pt)
2.3. Le caractère de l’amine mis en évidence est caractère nucléophile (0,5pt)
3.1 Formule générale des α-aminés (0,5 pt)
$\begin{array}{*{20}{c}}{R - }&{CH}&{ - COOH}\\{}&|&{}\\{}&{N{H_2}}&{}\end{array}$
3.2 Formule brute de l’acide α-aminé : en posant $R = {C_n}{H_{2n + 1}}$, on a : $M = 14n + 75$ $= 131$
$n = 4$(0,5 pt)
d’où la formule brute ${C_6}{H_{13}}{O_2}N$ (0,5 pt)
3.3 Formule semi-développée de l’acide α-aminé (0,5pt)
$\begin{array}{*{20}{c}}{{H_3}C - }&{CH}&{ - C{H_2} - }&{CH}& - &{COOH}\\{}&|&{}&|&{}&{}\\{}&{C{H_3}}&{}&{N{H_2}}&{}&{}\end{array}$
Acide –amino 4-méthylpentanoïque (0,5pt)

Exercice 2 : Acides-Bases /06pts
1. Un acide fiable est un acide qui se dissocie partiellement dans l’eau (0,5pt)
2.1. Calcule de $[{H_3}{O^ + }]$
$pH =$ $- \log ([{H_3}{O^ + }])$ $\Rightarrow$ $[{H_3}{O^ + }] = {10^{ - pH}}$(0,25pt)
AN : $[{H_3}{O^ + }] =$ ${10^{ - 3,4}} \approx$ $4 \times {10^{ - 4}}$ mol/L (0,25 pt)
2.2 Montrons que l’acide éthanoïque est acide faible (0,5 pt)
$[{H_3}{O^ + }] = 4 \times {10^{ - 4}}$ mol/L ${C_2} = {10^{ - 2}}$ mol/L
$[{H_3}{O^ + }] \prec {C_2}$ donc $C{H_3}COOH$ est un acide faible
2.3 Équation bilan de l’acide éthanoïque avec de l’eau (0,75pt)
$C{H_3}COOH$ $+ {H_2}O$ $\mathbin{\lower.3ex\hbox{\(\buildrel\textstyle\rightarrow\over{\smash{\leftarrow}\vphantom{_{\vbox to.5ex{\vss}}}}\)}}$ $C{H_3}CO{O^ - }$ $+ {H_3}{O^ + }$
2.4 Calcule de la concentration des espèces en solution
Espèces en solution :
Ions : ${H_3}{O^ + }$ , $C{H_3}CO{O^ - }$ , $H{O^ - }$
Molécules : $C{H_3}COOH$, ${H_2}O$
$2{H_2}O$ $\mathbin{\lower.3ex\hbox{\(\buildrel\textstyle\rightarrow\over{\smash{\leftarrow}\vphantom{_{\vbox to.5ex{\vss}}}}\)}}$ ${H_3}{O^ + }$ $+ H{O^ - }$
$[{H_3}{O^ + }][H{O^ - }]$ $= Ke$
$[H{O^ - }] = 2,5 \times {10^{ - 11}}$ mol/L (0,25pt)
$[{H_3}{O^ + }] \approx$ $[C{H_3}CO{O^ - }]$ $= 4 \times {10^{ - 4}}$ mol/L
$[C{H_3}COOH] +$ $[C{H_3}CO{O^ - }] =$ ${C_2}$
$[C{H_3}COOH]$ $= 9,6 \times {10^{ - 3}}$ mol/L (0,25pt)
- pKa de l’acide
$pH = pKa$ $+ \log \frac{{[C{H_3}CO{O^ - }]}}{{[C{H_3}COOH]}}$
$pKa \approx 4,8$ (0,25pt)
3. Dosage acide/base
3.1 Calcule de Ca
${n_a} = {n_b}$ $\Leftrightarrow$ ${C_a}{V_a} = {C_b}{V_b}$ (0,25pt)
${n_a} = {n_b}$ $\Leftrightarrow$ ${C_a} = \frac{{{C_b}{V_b}}}{{{V_a}}}$
${C_a} = 0,2$ mol/L (0,25 pt)
3.2 Calcule de la masse molaire (1 pt)
$C = \frac{n}{V}$ $= \frac{m}{{MV}}$ $\Rightarrow M =$ $\frac{m}{{CV}} = 102$ mol/L
Formule brute de l’acide
$M =$ $14n + 32 =$ $102 \Rightarrow$ $n = 5$
D’où la formule brute est : ${C_5}{H_{10}}{O_2}$

Exercice 3 : Chimie générale /4points
1.1. Niveau d’’énergie
L’énergie d’ionisation est l’énergie minimale à fournir à un atome pris dans son état fondamental afin de lui arracher son électron.
1.2.1 Il y a absorption des photons parce que l’électron passe d’énergie inférieur (n=1) aa un niveau d’énergie supérieur (p˃1)
Posons ${E_0} = 13,6eV$
$\Delta E = Ep$ $- En \Rightarrow$ $\upsilon = \frac{{13,6}}{h}$ $\left( {1 - \frac{1}{{{p^2}}}} \right)$ (0,5pt)
1.2.3. Calcule de $\upsilon$ pour $p = 3$
$\upsilon = 2,92 \times {10^{15}}$ Hz
2. Cinétique chimique
2.1 Montrons que les ions ${I^ - }$ sont en excès
$\frac{{{n_{{H_2}{O_2}}}}}{1} = \frac{{{C_1}{V_1}}}{1}$ $\Rightarrow$ ${n_{{H_2}{O_2}}} =$ $4,5 \times {10^{ - 3}}$ mol
$\frac{{{n_{{I^ - }}}}}{2} =$ $\frac{{{C_2}{V_2}}}{1} = {10^{ - 2}}$ mol
$\frac{{{n_{{I^ - }}}}}{2} \succ \frac{{{n_{{H_2}{O_2}}}}}{1}$
Donc les ions ${I^ - }$ sont en excès
2.2. On ajoute la glace pour bloquer la réaction d’oxydation des ions iodure par l’eau oxygénée dans le bécher (0,5 pt)
2.3. L’expression de la concentration de ${I_2}$
Équation de réaction
${I_2} +$ $2{S_2}O_3^{2 - }$ $\to$ $2{I^ - } +$ ${S_4}O_6^{2 - }$
A l’équivalence,
$\frac{{{n_{{I_2}}}}}{1} = \frac{{{n_{{S_2}O_3^{2 - }}}}}{2}$ $\Rightarrow [{I_2}]V$ $= \frac{{[{S_2}O_3^{2 - }]}}{2}{V_{{S_2}O_3^{2 - }}}$
${[{S_2}O_3^{2 - }] = C'}$ et ${V_{{S_2}O_3^{2 - }}} = V'$ On a dont
$[{I_2}] = \frac{{C'}}{{2V}}V'$ (0,25pt)
2.4. Calcule de la concentration ${[{I_2}]_t}$ à la fin de la réaction
${H_2}{O_2} +$ $2{I^ - } +$ $2{H_3}{O^ + }$ $\to$ ${I_2} +$ $4{H_2}O$
L’eau oxygénée étant le réactif en défaut sera totalement consommé à la fin de la réaction. Dans le bêcher, on a :
${[{I_2}]_t} = \frac{{{{({n_{{I_2}}})}_{formée}}}}{{{V_1} + {V_2}}}$
Or ${({n_{{I_2}}})_{formée}}$ $= {({n_{{H_2}{O_2}}})_{disparu}}$ $= {C_1}{V_1}$
${[{I_2}]_t} =$ $= \frac{{{C_1}{V_2}}}{{{V_1} + {V_2}}}$ $= \frac{{{C_1}}}{2}$ car ${{V_1} = {V_2}}$
${[{I_2}]_t} = 2,25 \times {10^{ - 2}}$ mol/L à la fin de la réaction

Exercice 4 : Caractère expérimental /4 points
1.1 Calcule du volume V0 de la solution à prélever, En appliquant la loi de la dilution, on a :
${C_0}{V_0} = CV$ $\Rightarrow {V_0} = \frac{{CV}}{{{C_0}}}$ (0,5pt)
${V_0} = 10$ mL
1.2. Deux éléments nécessaires pour la préparation
La fiole jaugée de 250 Ml et la pipette jaugée de 10 Ml
1.2 Mode opératoire
A l’aide d’une pipette jaugée de 10 mL, prélever 10 mL de la solution S0 et l’introduire dans une fiole jaugée de 250 mL contenant au préalable une quantité d’eau distillée. Complétons le volume dans la fiole jaugée avec l’eau distillée jusqu’au trait de jauge et homogénéiser.
2. Vérification de la concentration
2.1. Construction du diagramme $pH = f(Vb)$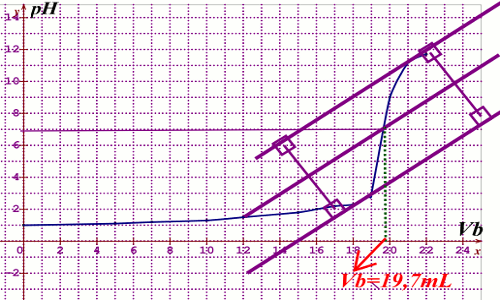
2.2. En utilisant la méthode des tangentes, on trouve à l’équivalence un volume $Vb = 19,7$ d’hydroxyde de sodium. (voir millimétrée)
2.3. Calcule de $Ca$
A l’équivalence
$Ca = \frac{{VbCb}}{{Ca}} = 0,098$ mol/L
2.4. $Ca \approx C = 0,1$ mol/L
Le dosage a permis de vérifier que la solution S d’acide chlorhydrique a été bien préparée