TC 2021 PHYSIQUE

ENNONCE

Partie l; Évaluation des ressources / 24 points

Exercice 1 Vérification des savoirs / 8 points

1. Définir : Effet photoélectrique, oscillation harmonique. 2 pt
2. Donner les unités SI des grandeurs physiques suivantes : période radioactive, champ magnétique. 1 pt
3. Énoncer la loi de Coulomb et la loi de gravitation universelle. 1,5 pt
4. Répondre par vrai ou faux aux propositions suivantes : 1 pt
(i) A la résonance d'intensité, l'impédance Z d'un circuit RLC est égale à la résistance totale R du circuit.
(ii) Le niveau fondamental est le niveau d'énergie le plus bas de l'atome.
5. QCM. Trouver la proposition vraie 1,5pt
5.1 L'équation différentielle d'un oscillateur élastique non amorti est de la forme :
(i) $\ddot x + \frac{k}{m}x = 0$;
(ii) $\ddot x + \frac{k}{m}x +$ $\frac{f}{m} = 0$;
(iii) $\ddot x + \frac{k}{m}x$ $- \frac{f}{m} = 0$;
(iv) $\ddot x + \frac{k}{m}x$ $+ \frac{m}{f} = 0$.
5.2 La célérité C d'un signal le long d'une corde a pour expression :
(i) $C = \sqrt {\frac{F}{\mu }}$ ;
(ii) $C = \sqrt {\frac{\mu }{F}}$ ;
(iii) $C = \frac{\mu }{F}$;
(iv) $C = \sqrt {F.\mu }$.
F : la tension de la corde et $\mu$ : la masse par unité de longueur de la corde.
5.3 Lors de l'effet Compton, le photon diffusé :
(i) est plus lent que le photon incident;
(ii) est plus rapide que le photon incident;
(iii) est plus énergétique que le photon incident ;
(iv) est moins énergétique que le photon incident
(v) a une masse inférieure à celle du photon incident.
6.Citer une application de l'effet photoélectrique. 1pt

Exercice 2 : Application des savoirs I 8 points

(Les parties A, 8 et C sont indépendantes)

Partie A : champ de gravitation / 2 points

La Terre et la Lune sont deux astres assimilés à des points matériels. Ils sont distants de $d = 3,8 \times {10^8}$ m.
1. Représenter le vecteur champ de gravitation crée sur la Lune par la Terre. 1 pt
2. Déterminer l'intensité du champ de gravitation crée par la Terre sur la Lune. 1 pt
On donne : la masse de la terre ${m_T} = 6,0 \times {10^{24}}$ kg;
La constante gravitationnelle $G = 6,67 \times {10^{ - 11}}$ N.m2/kg²

Partie B : Mouvement d'un solide sur un plan incliné / 3 points

Un corps supposé ponctuel dévale sans vitesse initiale un plan incliné d'un angle $\alpha$ sur l’horizontal. Les forces de frottements sont négligeables.
1. Faire le schéma et représenter les forces qui s'appliquent sur le corps 1 pt
2. Déterminer l'accélération du mouvement et déduire sa nature. 1 pt
On donne : g = 9,80 N/kg ; $\sin \alpha = 0,10$

Partie C : La propagation d'un mouvement vibratoire / 3 Points.

Une particule placée à la surface d'une eau au repos est traversée par une perturbation.
L'équation du mouvement de la particule est de la forme $x(t) =$ $a\sin \left( {\omega t} \right)$. Sa trajectoire est un segment de droite de 12 cm de longueur. A l'instant initial, la particule passe par la position d'équilibre et se déplace dans le sens positif des élongations. La période du mouvement est de 8s
Déterminer:
1. Les valeurs des constantes $a$ et $\omega$. 1 pt
2. L'expression de la vitesse du mobile. 1 pt
3. Le temps minimale au bout duquel l’élongation sera nulle, la particule allant dans le sens positif 1 pt

Exercice 3 : Utilisation des savoirs / 8 points

(Les parties A et 8 sont Indépendantes)

Partie A : Pendule élastique / 4 points

On suspend un solide de masse m = 200 g à l'extrémité inférieure d'un ressort vertical à spires non jointives de masse négligeable. Ce dernier a son extrémité supérieure fixé à un crochet fixe. À l'équilibre, le centre d'inertie du solide se trouve au point o, origine d'un axe vertical Ox descendant. On donne : g = 9,80 m/s²
On étire le ressort d'une distance $Xm = + 4,00$ cm et on l'abandonne sans vitesse initiale.
La constante de raideur du ressort est $K = 50,0$ N/m. Au cours de son mouvement, le centre d'inertie du solide est repéré par son abscisse x.
1.Faire l'inventaire des forces extérieures au solide à l'équilibre et déterminer l'allongement Xo du ressort. 1 pt
2. En appliquant le théorème du centre d'inertie au solide à un instant quelconque, établir l'équation différentielle de son mouvement. 1 pt
3. En déduire la période des oscillations du pendule élastique. 1 pt
4. En prenant pour origine des dates, le moment où le système est abandonné à lui-même, écrire l'expression de l’élongation $x(t)$. 1 pt

Partie B : Désintégration: radioactives successives / 4 points

On considère les deux noyaux suivants ${}_{92}^{238}U$ et ${}_{82}^{206}Pb$
1. Calculer pour chacun de ces noyaux, l'énergie de liaison moyenne par nucléon en MeV par nucléon. 1,5 pt
2. Quel serait le noyau le plus stable ? 0,5 pt
3. L'Uranium 238 subit plusieurs désintégrations successives de type $\alpha$ et de type ${\beta ^ - }$ et se transforme en Plomb 206.
Déterminer le nombre x de désintégrations $\alpha$ et y de désintégrations ${\beta ^ - }$ pour cette transformation. 1 pt
On donne : masse du proton : 1,00727 u ; masse de neutron : 1,00355 u : masse du noyau de plomb 206 : 205.9295 u ; masse du noyaux d'uranium : 238,035 u, 1u = 931 MeV/C²

Partie II : Évaluation des compétences / 16 points

Barème
Série C			Série E
Situation Problème	Question	Barème	Situation Problème	Question	Barème
1	1	3 pts	2		16 pts
	2	5 pts
2	1	8 pts

Situation problème 1: Série C et E
Dans votre ville, se jouent les qualifications pour le championnat national de lancer de poids.
Pour garantir l'équité, les organisateurs installent un ordinateur qui permet de modéliser le mouvement du projectile de chaque participant (document 1 let de détecter la hauteur de lancement H. Le document 2 présente la performance du candidat de votre quartier.
Pour se qualifier, Il faut que la distance entre O (origine du repère) et le point d'impact A soit supérieure à 15 m.
Les qualifications doivent se jouer lorsque le temps est beau, le projectile est alors en chute libre.
Le projectile est supposé ponctuel.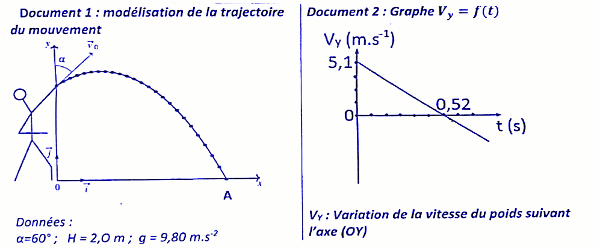
En utilisant les informations ci-dessus.
1. Vérifie si le temps est favorable pour tenir cette compétition.
2. Prononce-toi sur la qualification du représentant de votre quartier.

Situation problème 2: Série C / 8 points
Un vendeur de composant électronique reçoit très souvent les plaintes de ses clients sur la qualité des pièces et décide de vérifier les caractéristiques des pièces restantes dans le magasin
(Document)
Il fait appel à sa fille Angélique élève en classe de terminale C pour l'aider à faire ce travail. Une fois au laboratoire de l'établissement l'élève réalise les expériences suivantes :
Document : Composants disponibles dans le magasin.
Résistor ($R = 85\Omega$ ), bobine (1,2 H ; $15\Omega$); condensateur ($C = 6\mu F$)

Expérience 1
Elle monte le résistor aux bornes d'un générateur de tension constante U= 6 V, l'intensité du courant est alors I = 0,0706 A.

Expérience 2
Elle monte la bobine et le résistor en série. Ce circuit est alimenté par un générateur de tension constante U= 6 V. l'intensité du courant est alors I = 0,06 A.

Expérience 3
Elle monte le condensateur initialement déchargée en série avec le résister. Ce circuit est alimenté par un générateur de tension constante. Un dispositif approprié a permis de constater que la constante de temps du dipôle est $\tau = 0,5$ ms.

Expérience 4
Le résister, la bobine et le condensateur sont montés en série et alimentés par un générateur basse fréquence (GBF) qui délivre une tension sinusoïdale. Un oscillographe est branché et permet de suivre les variations des deux tensions.
On fait varier la fréquence délivrée par le GBF dans le circuit, les deux courbes obtenues sur l’oscillographe sont en phase. L'intensité du courant dans le circuit est de la forme : $i(t) = {I_m}$ $\cos \left( {136\pi t} \right)$
En exploitant les informations ci-dessus et partir d'un raisonnement logique , propose à Angélique la réponse qu'elle doit donner à son père.

CORRECTION

Partie l : Évaluation des ressources / 14 points

Exercice l : Vérification des savoirs /8 points

I. Définitions :

I Effet photoélectrique : extraction des électrons d'un métal par un rayonnement électromagnétique convenable. 1 pt
Oscillation harmonique : oscillation dont la loi horaire est une fonction sinusoïdale du temps. 1 pt
2. Unités SI:
Période radioactive : seconde 0,5 pt
Champ magnétique: tesla 0,5 pt
3. Énoncé de :
La loi de Coulomb : La force d’attraction ou de répulsion qui s’exerce entre deux charges ${q_A}$ et ${q_B}$, placees respectivement aux points A et B est dirigée suivant la droite $\left( {AB} \right)$, proportionnelle à ${q_A}$ et ${q_B}$, inversement proportionnelle au carrée de la distance qui sépare les deux charges. 0,75 pt
Loi de gravitation universelle : Deux corps ponctuels A et B, de masse respectives ${m_A}$ et ${m_B}$, exercent l’un sur l’autre des forces des forces d’attraction directement opposées, dirigées suivants la droite $\left( {AB} \right)$, proportionnelle aux masses ${m_A}$ et ${m_B}$ et inversement proportionnelle au carré de la distance qui les sépare. 0,75 pt
4. Vrai ou faux :
(i) À la résonance d'intensité, l'impédance $Z$ d'un circuit RLC est égale à la résistance totale R du circuit : Vrai 0,5 pt
(il) Le niveau fondamental est le niveau d'énergie le plus bas d'un atome : Vrai 0,5 pt
5. QCM : Proposition vraie.
5.]. L'équation différentielle d'un oscillateur élastique non amorti est de la formte : (i) $\ddot x + \frac{k}{m}x = 0$ 0,5pt
5.2. La célérité C d'un signal le long d'une corde a pour expression (i) $C = \sqrt {\frac{F}{\mu }}$ 0,5 pt
5.3. Lors de l’effet Compton, le photon diffusé : (iv) est moins énergétique que le photon incident. 0,5 pt
6. Une application de l'effet photoélectriques : 1 pt
Phototransistor, photopile, photodiode, plaques solaires...

Exercice 2 : Application des savoirs / 8 points

Partie A : Champ de gravitation / 2 points

l. Représentation du vecteur champ de gravitation $\left( {{{\overrightarrow g }_T}} \right)$ créé sur la Lune par la Terre.
2. Intensité du champ de gravitation ${g_T}$ créé par lu Terre sur la Lune : 0,5 x 2 = 1 pt
${g_T} = G\frac{{{m_T}}}{d}$ $= 2,8 \times {10^{ - 3}}$ N/kg

Partie B: Mouvement d'un solide sur un plan incliné / 3 points

l. Schéma de la situation 0,5 pt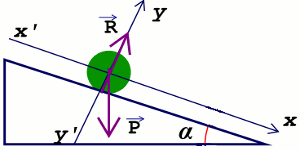
Dans le référentiel terrestre, le corps ponctuel subit deux forces :
• son poids $\overrightarrow P$ ; 0,5 pt
• la réaction $\overrightarrow R$ du plan. 0,5 pt
2. Accélération du monument.
D’après le TCI : $\sum {\overrightarrow {{F_{ext}}} = m\overrightarrow {{a_G}} }$ $\Leftrightarrow \overrightarrow P + \overrightarrow R$ $= m\overrightarrow {{a_G}}$ 0,5 pt
Par projection suivant l'axe (x'x) parallèle à in ligne de plus grande pente et orienté vers le bas, on obtient : 0,5 pt
${a_G} = g\sin \alpha$ $= 0,98$ m/s2
Nature du mouvement :
${a_G} = cte$ et la trajectoire est rectiligne, donc le mouvement est rectiligne uniformément accéléré. 0,5 pt

Partie C: La propagation d'un mouvement vibratoire / 3 points

I. Valeurs des constante: : 0,25 x 2 = 0,5 pt
Amplitude $a$ : $a = \frac{L}{2}$ $= 6cm$
Pulsation $\omega$ : $\omega = \frac{{2\pi }}{T}$ $= \frac{\pi }{4}$ rad/s
1. Expression de la vitesse du mobile : $\dot x(t) =$ $a\omega \cos \left( {\omega t} \right) =$ $\frac{3}{2}\pi \cos \left( {\frac{\pi }{4}t} \right)$ ( en cm/s) 1 pt
3. Temps minimal pour que l’élongation s'annule.
Contraintes : $x = 0$ et $\dot x(t) \succ 0$
Alors $\left\{ \begin{array}{l}\sin \left( {\omega t} \right) = 0\\\cos \left( {\omega t} \right) \succ 0\end{array} \right.$ $\Rightarrow t = 2k\frac{\pi }{\omega }$ ou $t = kT$, k étant un entier naturel non nul. 0,5 pt
Le temps est minimal pour $k = 1$ soit : ${t_{\min }} = T$ $= 8s$

Exercice 3 : Utilisation du savoirs / 8 points

Partie A : Pendule élastique / 4 points

l. Inventaire des forces
Dans le référentiel terrestre, le solide subit deux forces : son poids $\overrightarrow P$ et la tension $\overrightarrow T$ du ressort.
• Allongement ${x_0}$ du ressort à l’équilibre.
Condition d'équilibre : $\overrightarrow P + \overrightarrow T = \overrightarrow O$
Soit ${x_0} = \frac{{mg}}{k}$ $= 3,92$ cm
2. Équation différentielle.
D’après le TCI : $\overrightarrow P + \overrightarrow T = m\overrightarrow {{a_G}}$
Par projection suivant l'axe vertical (x'x) orienté vers le bas. on obtient : $\ddot x + \frac{k}{m}x = 0$ ou $\ddot x + 250x = 0$ 0,5 pt
3. Période ${T_0}$ des oscillations.
L'équation différentielle est de la forme $\ddot x + \omega _0^2x = 0$ soit ${\omega _0} = \sqrt {\frac{k}{m}}$
${T_0} = 2\pi \sqrt {\frac{m}{k}}$ $= 0,397$ s 0,5 pt x 2 = 1 pt
4. Expression de l’élongation x(t).
Forme générale : $x(t) = {X_m}$ $\cos \left( {{\omega _0}t + \varphi } \right)$
Conditions initiales : à $t = 0s$, $x = Xm$ et $\dot x = 0$ d'où $\varphi = 0$ 0,25 pt
Avec Xm = 4,00 cm et ${\omega _0} = 15,8$ rad/s
Finalement $x(t) =$ $4\cos \left( {15,8t} \right)$ ( en cm) 0,5 pt

Partie Il : Désintégrations radioactives successives / 4 points

l. Énergie de liaison moyenne par nucléon
• Noyau d'uranium 238:
${E_U} =$ $\frac{{\left| {92{m_p} + 146{m_n} - {m_U}} \right|}}{{238}}$ ${c^2}$ 0,5 pt
AN : ${E_U} = 7,23$ MeV/nucléon 0,25 pt
• Noyau de plomb
${E_{Pb}} =$ $\frac{{\left| {82{m_p} + 124{m_n} - {m_{Pb}}} \right|}}{{206}}$ ${c^2}$ 0,5 pt
AN : ${E_Pb} = 7,87$ MeV/nucléon 0,25 pt
2. Le noyau le plus stable est ${}_{82}^{206}Pb$, 0,5 pt
3. Nombre $x$ de désintégrations $\alpha$ et $x$ de désintégrations ${\beta ^ - }$.
Équation bilan de la transformation
${}_{82}^{238}U \to {}_{92}^{206}Pb$ $+ x{}_2^4He$ $+ y{}_{ - 1}^0e$ 0,5 pt
(Lois de Soddy) Conservation du nombre de masse et du nombre de charge : $\left\{ \begin{array}{l}238 = 206 + 4x\\92 = 82 + 2x - y\end{array} \right.$
On trouve x = 8 et y = 6. 0,5 x 2 = 1 pt

Partie Il : Évaluation des compétences / 16 points

Situation Problème 1 : Série C

Vérification si le temps est favorable.
Il s'agit de vérifier si le temps est favorable en examinant si le projectile est en chute libre.
Pour cela nous allons :
• supposer que le projectile est en chute libre, puis exploiter le document l pour donner la nature du mouvement suivant les deux axes ;
• Exploiter le document 2 pour déterminer la valeur de l'accélération ${a_G}$ du mouvement lors du concours ;
• La comparer à la valeur de l'accélération dans le cas d'une chute libre et conclure.

Supposons que le projectile est en chute libre.
1.1 Détermination de la nature du mouvement du projectile.
Le document (l) montre que la trajectoire du projectile est un arc de parabole contenu dans le plan du tir.
Le mouvement du projectile est :
• Uniforme suivant l'axe $\left( {0;\overrightarrow i } \right)$;
• uniformément varie suivant l'axe $\left( {0;\overrightarrow j } \right)$ .
1.2. Détermination de la valeur de l'accélération du mouvement.
On a ${a_x} = 0$; $a_{y}=\frac{\Delta v_{y}}{\Delta t}$ soit ${a_G} =$ $\sqrt {{a_x} + {a_y}}$ $= 9,81$ m/s2
1.3. Comparaison:
Accélération du mouvement : ${a_G} = 9,81$ m/s2 alors que g=9,80m/s2.
La différence entre ${a_G}$ et $g$ est négligeable ; on peut donc écrire ${a_G} = g$
Conclusion : Comme ${a_G} = g$, le projectile est en chute libre, donc le temps est favorable pour tenir cette compétition.

2. Examen d'une éventuelle qualification du représentant du quartier.
Il s'agit de déterminer la distance $OA$ afin de se prononcer sur la qualification du candidat.
Pour cela :
• Établir les équations horaires du mouvement ;
• Déterminer l'abscisse X = 0A du point d'impact A du projectile avec le sol horizontal ;
• Comparer au minimum requis et conclure.
2.1 Détermination des équations libraires du mouvement
Dans le référentiel terrestre supposé galiléen, le projectile est soumis uniquement à l’action de son poids $\overrightarrow P$
$\overrightarrow v \left| \begin{array}{l}{v_0}\sin \alpha \\ - gt + {v_0}\cos \alpha \end{array} \right.$. Par intégrations successives, on obtient $\overrightarrow {OG} \left| \begin{array}{l}x(t)\\y(t)\end{array} \right.$ avec $x(t) =$ $\left( {{v_0}\sin \alpha } \right)t$ (1) et $y(t) = - \frac{1}{2}g{t^2} +$ ${v_0}t\cos \alpha + H$
Équation de la trajectoire
De (1), $t = \frac{x}{{{v_0}\sin \alpha }}$ soit $y(x) = -$ $\frac{1}{2}g\frac{{{x^2}}}{{v_0^2{{\sin }^2}\alpha }}$ $+ \frac{{{v_0}}}{{\tan \alpha }} + H$
2.2 Détermination de l'abscisse X du point d’impact A avec le sol horizontal
Valeur de la vitesse initiale ${v_0}$
En exploitant le document 2. on obtient : ${v_0}\cos \alpha =$ $5,1 \Rightarrow {v_0} =$ $\frac{{5,1}}{{\cos \alpha }} = 10,2$ 10,2 m/s
On peut donc écrire : $y(x) = - 0,063{x^2}$ $+ 0,577x + 2$
Au point A. $y(X) =$ $- 0,063{X^2} +$ $0,577X + 2 = 0$
On trouvera après résolution X = 0A = 11,8 m
2.3 Comparaison:
Pour une qualification. ${X_{\min }} = 15$
On constate que $OA \prec {X_{\min }}$
Conclusion : Comme la distance 0A ne répond pas aux conditions requises, le représentant du quartier ne s‘est pas qualifié.

Situation Problème 2 : Série C

Avis sur les caractéristiques des composants électroniques
Il s'agit de déterminer les caractéristiques réelles des pièces afin d'apprécier leur qualité.
Pour cela, nous allons 2
• Exploiter les résultats des expériences pour déterminer :
La résistance du résister ;
La résistance de la bobine ;
La capacité du condensateur :
L’inductance de la bobine.
• Comparer aux valeurs inscrites ct conclue.
l. Exploitation de l'expérience l.
Détermination de la résistance (R) du résistor
D'après la loi d'Ohm. $R = \frac{U}{I}$ $= 85\Omega$
2. Exploitation de l'expérience 2.
Détermination de la résistance (r) de la bobine.
$U = \left( {R + r} \right)I$ $\Rightarrow r = \frac{U}{I} -$ $R = 15\Omega$
3. Exploitation de l'expérience 3.
Détermination de la capacité (C) du condensateur.
Le dipôle constitué en série d'un résister et d'un condensateur, alimenté par une tension constante, donne lieu à un régime transitoire de constante de temps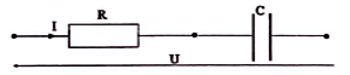
$\tau = RC \Rightarrow C$ $= \frac{\tau }{R} = 6 \times$ ${10^{ - 6}}F$
4. Exploitation de l'expérience 4.
Détermination de l’inductance (L) de la bobine.
• Le dipôle RLC ainsi constitué est en oscillations forcées.
• Comme les tensions $u$ et ${u_R}$ sont en phase, il s’agit d'une résonance d’intensité.
• Condition de résonance :
$LC\omega _0^2 = 1$ $\Rightarrow L =$ $\frac{1}{{C\omega _0^2}} = 0,91H$
5. Comparaison:

Composant	Caractéristiques		Observation
	Inscrites	obtenus expéri mentalement
Résistor	R = 85 $\Omega$	${{\mathop{\rm R}\nolimits} _{exp}} = 85\Omega$	Valeurs identiques
Bobine	$r = 15\Omega$ $L = 1,2H$	${r_{\exp }} = 15\Omega$ ${L_{\exp }} = 0,91H$	Même valeur de la résistance, mais les valeurs de l’inductance sont différentes
Conden sateur	$C = 6F$	${C_{\exp }} = 6F$	Valeurs identiques

Conclusion :
• Au regard des caractéristiques des composants vendus :
le résistor et le condensateur sont de bonne qualité ;
la bobine n'est pas de bonne qualité.