ENNONCE
Partie A : Évaluation des ressources : 15 points
Exercice 1 : 5,5 points pour la série C et 4 points pour la série C
I- (Série C exclusivement)
On considéré la droite \(\left( D \right)\) d’équation réduite \(y = \frac{{65}}{{16}}x - \frac{5}{{16}}\) dans un repère orthonormé du plan.
1. Démontrer que (D) passe par au moins un point M dont les coordonnées sont des nombres entiers relatifs. 0,25 pt
2. Déterminer l'ensemble E des points de (D) à coordonnées entières. 0,75 pt
3. Déterminer les points de (D) dont les ordonnées sont des entiers compris entre -126 et 134 0,5 pt
II Soit un point \(A\left( { - 2;1;1} \right)\) et un vecteur \(\overrightarrow n \left( {1; - 2,3} \right)\) de l'espace \(\varepsilon \) muni d'un repère orthonormé \(\left( {O;\overrightarrow i ;\overrightarrow j ;\overrightarrow k } \right)\).
1. Déterminer une équation du plan (P) contenant le point A et de vecteur normal \(\overrightarrow n \). 0,5 pt
2. Donner une expression analytique de la réflexion de plan (P). 1 pt
III- Le plan complexe est rapporté à un repère \(\left( {O;\overrightarrow u ;\overrightarrow v } \right)\). On considère la transformation \(g\) du plan d'écriture complexe \(Z' = \frac{{1 + i}}{2}\) \(Z + 1\).
\(\Omega \) est le point d'affixe \({1 + i}\). les points \(An\) d'affixes \(Zn\)
\(\left( {Zn} \right)\) est la suite définie par : \({Z_0} = 0\) et \({Z_{n + 1}} = 1 + \) \(\frac{{1 + i}}{2}{Z_n}\) pour tout entier naturel \(n\).
1. Déterminer la nature et les éléments caractéristiques de \(g\). 1 pt
2. Montrer que :
a) Pour tout entier naturel \(g\), les points \(\Omega {A_n}\) et \({A_{n + 4}}\) sont alignés. 0,5 pt
b) Pour tout entier naturel \(g\). le triangle \(\Omega {A_n}{A_{n + 1}}\), est rectangle et isocèle. 1 pt
Exercice 2 : 4,5 points
l- Une urne contient 6 boules indiscernables au toucher dont deux boules sont marquées 0, trois boules sont marquées \(\sqrt 3 \) et une boule marquée \( - \sqrt 3 \). On tire successivement et sans remise deux boules de cette urne.
On note \(\lambda \) la variable aléatoire qui à chaque tirage associe la somme des nombres marqués sue les boules tirées.
1. Déterminer la loi de probabilité de \(\lambda \). 0,75 pt
2. Calculer l'espérance mathématique et l'écart-type de \(\lambda \) 0,75 pt
II Le plan est muni d'un repère orthonormé direct \(\left( {O;\overrightarrow i ,\overrightarrow j } \right)\).
\(\left( \Sigma \right)\) est l'ensemble des points \(M\left( {X;Y} \right)\) tels que \(4{X^2} - {Y^2} = \) \( - 4\).
1. Déterminer la nature et les éléments caractéristiques de \(\left( \Sigma \right)\). 1 pt
\(r\) est la rotation de centre O et d'angle \( - \frac{\pi }{6}\)
2. a) Donner l'expression analytique de \(r\) 0,75 pt
b) Déterminer une équation de l'ensemble \(\left( {\Sigma '} \right)\), image de \(\left( {\Sigma} \right)\) par \(r\) 0,5 pt
b) Déterminer la nature et les éléments caractéristiques de \(\left( {\Sigma '} \right)\).
c) Construire dans le repéré \(\left( {O;\overrightarrow i ,\overrightarrow j } \right)\), \(\left( {\Sigma} \right)\) et \(\left( {\Sigma '} \right)\). 0,5 pt
Exercice 3 : 3,25 points pour la série C et 4,75 points pour la série E.
On considère une fonction numérique \(f\) définie sur \(\mathbb{R}\) par \(f(x) = \frac{{x + 2}}{{{e^x}}}\) et \(\left( C \right)\) sa courbe représentative dans un repéré orthonormé : unité sur les axes : 2 cm
1. a) Étudier les variations de \(f\). 0,75 pt
b) Déterminer une équation cartésienne de la tangente (T) en (C) au point d'abscisse - 1. 0,25 pt
c) Construire la courbe (C) de \(f\) et (T) dans le même repère. 1 pt
2. a) Déterminer les constante réelles a, b et c telles que la fonction \(F\) définie \(\mathbb{R}\) par \(F(x) = \frac{{ax + b}}{{{e^x}}}\)\(F(x) = \frac{{ax + b}}{{{e^x}}}\) \( + cx\) soit une primitive de \(f\) . 0,75 pt
b) Calculer \(\int\limits_{ - 1}^0 {f(x)dx} \) 0,5pg
3. (E exclusivement)
On considère la fonction numérique \(f\) définie sur n par \(h(x) = f( - x)\), \(\left( {C'} \right)\) sa courbe et (E) l'équation différentielle définie par : \(y'' - 2y'\) \( + y = 0\).
a) Résoudre (E). 0,75 pt
b) Déterminer la solution de (E) dont la courbé passe par le point A(0 ; -1) et admet en ce point une tangente de coefficient directeur 1. 0,75 pt
Partie B : Évaluation des compétences : 5 points
Situation :
La figure ci-après représente le domaine d'un villageois nommé ABBA.
Il a cultivé cette année des carottes et des pastèques dans des portions comme l'indique la figure ci-dessus.
Il a recolle le même jour et a tout déversé dans un camion. Son fils KAM met en sac afin de vendre à raison de BBOOF le sac de pastèques et à 3000F le sac de carottes, pour un total de 17 sacs.
A la fin de la vente, ABBA appelle KAM au téléphone pour savoir la recette obtenue. Avec des problèmes de réseau il le suit à peine et ne retient que : « la différence entre le prix de vente total des carottes et des pastèques n'est que de 4000F ». Un sac de chaque type n'est pas vendu.
ABBA envisage vendre une partie ou tout son vaste terrain à l'avenir. Dans cette zone, le m“ coute 2000F. Il confie ce projet à M KONG pour l'estimation de la valeur de ce terrain. Celui-ci crée un repère indiqué sur la figure ci-dessus où l'unité sur l'axe des ordonnées est 10m et 100m sur l'axe des abscisses. Les contours du terrain sont constitués de la droite (AB), la droite (DB) et la ligne (C).
La droite (L) représente la séparation de la portion exploitée pour cultiver les pastèques de celle exploitée pour cultiver les carottes. KONG a réussi à trouver les équations de (C) et de (L) qui sont respectivement \(y = \frac{{{e^x} - {e^{ - x}}}}{{{e^x} + {e^{ - x}}}}\) et \(y = \frac{1}{4}x\).
Tâches :
1. Combien coûtera ce terrain entier que ABBA souhaite vendre ? 1,5 pt
2. Combien aura ABBA s'il ne souhaite vendre que la portion réservée aux pastèques ? 1,5pt
3. Aider ABBA à retrouver le nombre de secs de chaque type des deux produits cultivés. 1,5pt
Présentation : 0,5pt
CORRECTION
bonjour bonjour bonjour bonjour bonjour bonjour
Partie A : Évaluation des ressources (15 points)
Exercice 1 : 5,5 points (C) / 4 points (E)
I- (Série C exclusivement)
1. Démontrons que (D) passe par au moins un point M dont les coordonnées sont des nombres entiers relatifs. 0,25 pt
Soit \(M\left( {x;y} \right)\) un point du plan.
\(M \in \left( D \right)\) équivaut à \(y = \frac{{65}}{{16}}x - \frac{5}{{16}}\) équivaut à \(65x - 16y = 5\). Et puisque PGCD(65 ; 16) = 1, alors l'équation diophantienne \(65x - 16y = 5\) admet au moins une solution dans \(\mathbb{Z} \times \mathbb{Z}\).
2. Déterminons l'ensemble (E) des points de (D) à coordonnées entières.
(E) est l'ensemble des points dont les coordonnées sont les solutions de l'équation \(65x - 16y = 5\) dans \(\mathbb{Z} \times \mathbb{Z}\)
(5 ; 20) est une solution particulière de l'équation \(65x - 16y = 5\) et par conséquent\(65\left( {x - 5} \right) = \) \(16\left( {y - 20} \right)\). D'après le théorème de Gauss. il existe \(k \in \mathbb{Z}\) tel que \(x = 16k + 5\) et \(y = 65k + 20\). Donc \(\left( E \right) = \{ M(16k\) \( + 5;65k + 20),\) \(k \in \mathbb{Z}\} \) 0,75 pt
3. Déterminons les points de (D) dont les coordonnées sont des entiers compris entre -126 et 134.
Il s'agit des points M(x ;y) tels que \(x = 16k + 5\) et \(y = 65k + 20\) avec \( - 126 \le y \le 134\).
De \( - 126 \le y \le 134\), on a \(k \in \{ - 2;\) \( - 1;0;1\} \) et par conséquent, ces points ont pour
coordonnées (\(\left( { - 27; - 110} \right)\), \(\left( { - 11; - 45} \right)\), \(\left( { 5; 20} \right)\), et \(\left( { 21; 85} \right)\). 0,5 pt
II.1 Déterminons une équation du plan (P) contenant le point A et de vecteur normal \(\overrightarrow n \).
Soit M(x; y: z) un point de l'espace \(\varepsilon \).
\(M \in (P)\) de vecteur normal \(\overrightarrow n \left( \begin{array}{l}1\\ - 2\\3\end{array} \right)\) équivaut à \(x - 2y + \) \(3z + d = 0\). où \( d \) est un réel.
Par ailleurs \(A\left( \begin{array}{l} - 2\\1\\1\end{array} \right) \in P\) équivaut à \( - 2 - 2 + \) \(3 + d = 0\). d'où d = 1. Donc \(x - 2y + \) \(3z + 1 = 0\) est une équation du plan (P). 0,5 pt
Donnons une expression analytique de la réflexion de plan (P).
Soient M(x; y; z) et M‘(x’; y’; z‘) deux points de l’espace \(\varepsilon \).
M’ est l'image de M par cette réflexion : \(\left\{ \begin{array}{l}\overrightarrow {MM'} = \alpha .\overrightarrow n \\milieu\left[ {MM'} \right] \in \left( P \right)\end{array} \right.\) avec \(\alpha \in \mathbb{R}\)
\(\left\{ \begin{array}{l}x' = \alpha + x\\y' = - 2\alpha + y\\z' = 3\alpha + z\end{array} \right.\) avec \(\alpha \in \mathbb{R}\)
\(\frac{{x + x'}}{2} - \) \(2\frac{{y + y'}}{2} + \) \(3 \times \frac{{z + z'}}{2} = 0\)
Ainsi \(\alpha = - \frac{1}{7}x\) \( + \frac{2}{7}y - \frac{3}{7}z\) \( - \frac{1}{7}\) 1 pt
\(x' = \frac{6}{7}x + \) \(\frac{2}{7}y - \frac{3}{7}z\) \( - \frac{1}{7}\), \(y' = \frac{2}{7}x + \) \(\frac{3}{7}y + \frac{6}{7}z + \frac{2}{7}\) et \(z' = - \frac{3}{7}x + \) \(\frac{6}{7}y - \frac{2}{7}z - \frac{3}{7}\) est l'expression analytique de cette réflexion.
III.1 Déterminons la nature et les éléments caractéristiques de \(g\). 1 pt
Nature : \(g\) est une similitude directe.
Éléments caractéristiques :
• Centre : c'est le point d’affixe \(w = \frac{{ - 2}}{{ - 1 + i}}\) \( = 1 + i\), Donc le point \(\Omega \) est le centre.
• Rapport : \(k = \left| {\frac{{1 + i}}{2}} \right|\) \( = \frac{{\sqrt 2 }}{2}\)
• Angle: \(\theta = Arg\left( {\frac{{1 + i}}{2}} \right)\) \( = \frac{\pi }{4}\)
a) Montrons que pour tout entier naturel \(n\), les points \(\Omega \), \(A_n\) et \({A_{n + 4}}\) sont alignés.
Soit \(n\), un entier naturel.
1ere méthode :
\(Mes\left( {\widehat {\overrightarrow {\Omega {A_n}} ,\overrightarrow {\Omega {A_{n + 4}}} }} \right) = \) \(Mes\left( {\widehat {\overrightarrow {\Omega {A_n}} ,\overrightarrow {\Omega {A_{n + 1}}} }} \right) + \) \(Mes\left( {\widehat {\overrightarrow {\Omega {A_n}} ,\overrightarrow {\Omega {A_{n + 2}}} }} \right) + \) \(Mes\left( {\widehat {\overrightarrow {\Omega {A_n}} ,\overrightarrow {\Omega {A_{n + 3}}} }} \right) + \) \(Mes\left( {\widehat {\overrightarrow {\Omega {A_n}} ,\overrightarrow {\Omega {A_{n + 4}}} }} \right) \)
\(Mes\left( {\widehat {\overrightarrow {\Omega {A_n}} ,\overrightarrow {\Omega {A_{n + 4}}} }} \right) = \) \(4 \times \frac{\pi }{4} = \pi \) ainsi \), les points \(\Omega \), \(A_n\) et \({A_{n + 4}}\) sont alignés.
2e méthode :
De proche en proche, on établit que \({Z_{n + 4}} = - \frac{1}{4}{Z_n}\). Ainsi \({A_{n + 4}}\) est l’image de \({A_{n }}\) l‘homothétie de rapport \( - \frac{1}{4}\) et de centre \(\Omega \). Ainsi \), les points \(\Omega \), \(A_n\) et \({A_{n + 4}}\) sont alignés. 0,5 pt
b) Montrons que pour tout entier naturel \(n\). le triangle \(\Omega {A_n}{A_{n + 4}}\)est rectangle et isocèle.
Soit n un entier naturel.
\(\frac{{{Z_{n + 1}} - {Z_n}}}{{{Z_{n + 1}} - {Z_\Omega }}} = \) \(\frac{{1 + \frac{{1 + i}}{2}{Z_n} - {Z_n}}}{{1 + \frac{{1 + i}}{2}{Z_n} - 1 - i}}\) \( = i\), Donc le triangle \(\Omega {A_n}{A_{n + 1}}\) est rectangle et isocèle en \({A_{n + 1}}\) 1 pt
Exercice 2 : 5,25 points (C et E)
Déterminons la loi de probabilité de \(\lambda \).
L’univers image \(\lambda \left( \Omega \right) = \{ 0;\sqrt 3 ;\) \( - \sqrt 3 ;2\sqrt 3 \} \)
| \(k\) | \( - \sqrt 3 \) | 0 | \(\sqrt 3 \) | \(2\sqrt 3 \) |
| \(p\left( {\lambda = k} \right)\) | \(\frac{2}{{15}}\) | \(\frac{4}{{15}}\) | \(\frac{6}{{15}}\) | \(\frac{3}{{15}}\) |
2. Calculons de l’espérance mathématique et l'écart type de \(\lambda \).
L'espérance est : \(E\left( \lambda \right) = \) \(\sum {kP\left( {\lambda = k} \right)} \) \( = \) \(\frac{{6\sqrt 3 - 2\sqrt 3 + 6\sqrt 3 }}{{15}}\) \( = \frac{{2\sqrt 3 }}{{15}}\)
La variance est: \(V\left( \lambda \right) = \) \(\sum {{k^2}P\left( {\lambda = k} \right)} \) \( - {E^2}\left( \lambda \right)\) \( = \frac{8}{3}\)
II.1. Déterminons la nature et les éléments caractéristiques de \(\left( \Sigma \right)\).
Nature : \(\left( \Sigma \right)\) est une hyperbole.
Éléments caractéristiques : dans le repère \(\left( {O;\overrightarrow i ,\overrightarrow j } \right)\). 1 pt
• Centre : le point O.
• Sommets : \(B\left( {0;2} \right)\) et \(B'\left( {0; - 2} \right)\).
• Foyers : \(F\left( {0;\sqrt 5 } \right)\) et \(F'\left( {0; - \sqrt 5 } \right)\),
• Directrices: \(\left( \Delta \right)\) : \(Y = \frac{{4\sqrt 5 }}{5}\) et \(\left( {\Delta '} \right)\) : \(Y = - \frac{{4\sqrt 5 }}{5}\).
• Excentricité : \(e = \frac{{\sqrt 5 }}{2}\)
2. a) Donnons l'expression analytique de \(r\). 0,75 pt
Soient \(M\left( {X;Y} \right)\) et \(M'\left( {X';Y'} \right)\) deux points d'armes respectives \(z\) et \(z'\).
\(M' = r\left( M \right)\) \( \Leftrightarrow z = {e^{ - \frac{\pi }{6}i}}z \Leftrightarrow \) \(X' + iY' = \) \(\left( {\frac{{\sqrt 3 }}{2} - \frac{1}{2}i} \right)\) \(\left( {X + iY} \right)\)
Ainsi \(X' = \frac{{\sqrt 3 }}{2}X\) \( + \frac{1}{2}Y\) et \(Y' = - \frac{1}{2} + \) \(\frac{{\sqrt 3 }}{2}Y\). qui est l'expression analytique de la rotation \(r\). 0,75 pt
b) Déterminons une équation de l'ensemble \(\left( {\Sigma '} \right)\) image de \(\left( {\Sigma '} \right)\) par \(r\).
Soient M(X ; Y) et M(X’; Y’) deux points d'affixes respectives \(z\) et \(z’\).
\(X' = \frac{{\sqrt 3 }}{2}X\) \( + \frac{1}{2}Y\) et \(Y' = - \frac{1}{2}X + \) \(\frac{{\sqrt 3 }}{2}Y\) ainsi \(X = \frac{{\sqrt 3 }}{2}X'\) \( - \frac{1}{2}Y'\) et \(Y = - \frac{1}{2}X'\) \( + \frac{{\sqrt 3 }}{2}Y'\)
\(4{X^2} - {Y^2} = \) \( - 4 \Rightarrow 4\) \({\left( {\frac{{\sqrt 3 }}{2}X' - \frac{1}{2}Y'} \right)^2} - \) \(\left( { - \frac{1}{2}X' + \frac{{\sqrt 3 }}{2}Y'} \right)\) \( = - 4\)
\(11X{'^2} + Y{'^2}\) \( - 10\sqrt 3 X'Y' + \) \(16 = 0\) (1)
Donc, une équation de l'ensemble \(\left( {\Sigma '} \right)\) image de \(\left( {\Sigma } \right)\) par r est (1) 0,5 pt
c) Déterminons la nature et les éléments caractéristiques de \(\left( {\Sigma '} \right)\). 1 pt
• Nature : \(\left( {\Sigma '} \right)\) est une hyperbole.
• Éléments caractéristiques : dans le repère \(\left( {O;\overrightarrow i ,\overrightarrow j } \right)\)
• Centre : le point O.
• Sommets : \(S(1;\sqrt 3 )\) et \(S'( - 1; - \sqrt 3 )\).
• Foyers : \(r(F)\) et \(r(F’)\).
• Directrices : \(r(\Delta )\) et \(r(\Delta ')\).
• Excentricité : \(e = \frac{{\sqrt 5 }}{2}\)
d) Construisons dans le même repère \(\left( {O;\overrightarrow i ,\overrightarrow j } \right)\), \(\left( \Sigma \right)\) et\(\left( {\Sigma '} \right)\). 0,5 pt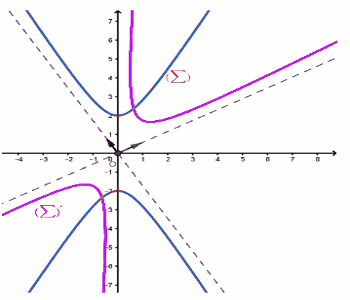
Exercice 3 : 3,25 points (C) / 4,75 points (E)
1. a) Étudions les variations de \(f\).
La fonction \(f\) est dérivable sur \(\mathbb{R}\) et pour tout \(x \in \mathbb{R}\), \(f'(x) = \) \(\frac{{\left( { - x - 1} \right){e^x}}}{{{e^{2x}}}}\) \( = \frac{{\left( { - x - 1} \right)}}{{{e^x}}}\)
Ainsi, \(f\) est strictement décroissante sur \(\left] { - 1; + \infty } \right[\) et strictement croissante sur \(\left] { - \infty ; - 1} \right[\). 0,75 pt
b) Déterminons une équation cartésienne de la tangente \(\left( T \right)\) en \(\left( C \right)\) au point d'abscisse \({ - 1}\).
\(\left( T \right):y = \) \(f'( - 1)(x + 1)\) \( + f( - 1)\). Donc une équation de \(\left( T \right)\) est \(y = e\)
c) Construisons la courbe \(\left( C \right)\) de \(f\) et \(\left( T \right)\) dans le même repère. 1 pt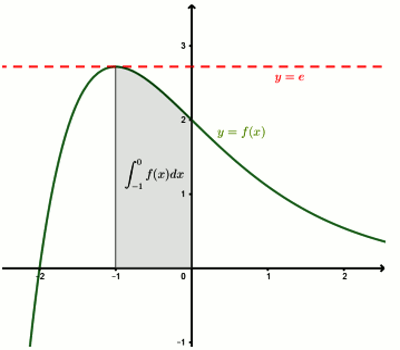
2. a) Déterminons les constantes réelles \(a\), \(b\) et \(c\) telles que la fonction \(F\) définie sur \(\mathbb{R}\) soit une primitive de \(f\).
\(F\) est une primitive de \(F\) sur \(\mathbb{R}\) si et seulement si \(F\) est dérivable sur \(\mathbb{R}\) et pour tout \(x \in \mathbb{R}\),
\(F'(x) = f(x)\), ainsi, pour tout \(x \in \mathbb{R}\), \(\frac{{ - ax + a - b + c{e^x}}}{{{e^x}}}\) \( = \frac{{x + 2}}{{{e^x}}}\) donc \(\left\{ \begin{array}{l}a = - 1\\b = - 3\\c = 0\end{array} \right.\) 0,75 pt
b) Calculons \(\int_{ - 1}^0 {f(x)dx} \).
\(\int_{ - 1}^0 {f(x)dx} = \) \(\left[ {\frac{{ - x - 3}}{{{e^x}}}} \right]_{ - 1}^0\) \( = - 3 + 2e\)
\(\int_{ - 1}^0 {f(x)dx} \) \( = - 3 + 2e\). 0,5 pt
3. (Série E exclusivement)
a) Résolvons \(\left( E \right)\).
l'équation caractéristique de \(\left( E \right)\) est \({r^2} - 2r\) \( + 1 = 0\) qui a pour solution \(r = 1\). Donc les solutions de l'équation \(\left( E \right)\) sont les fonctions U telles que pour tout \(x \in \mathbb{R}\),
\(U(x) = \) \(\left( {Ax + B} \right){e^x}\) avec A et B qui sont des constantes réelles par rapport à \(x\). 0,75 pt
b) Déterminons la solution de \(\left( E \right)\) dont la courbe passe par le point \(A\left( {0;1} \right)\) et admet en ce point une tangente de coefficient directeur 1.
Désignons par \(\left( G \right)\) cette solution. Alors \(G(0) = - 1\) et \(G'(0) = 1\) d'où \(B = - 1\) et \(A + B = 1\), donc \(G(x) = \) \(\left( {2x - 1} \right){e^x}\)
Partie B : Évaluation des compétences (5 points)
Références et solutions
Tâche 1 : Déterminons le coût de ce terrain entier que ABBA souhaite vendre.
Calculons en m2 l'aire \({A_1}\) de ce terrain entier
\({A_1} = \) \(\left( {\int_0^4 {\frac{{{e^x} - {e^{ - x}}}}{{{e^x} + {e^{ - x}}}}dx} } \right)\) \( \times 1000 = \) \(\left[ {\ln \left( {{e^x} + {e^{ - x}}} \right)} \right]_0^4\) \( \times 1000 = \) \(\ln \left( {\frac{{{e^4} + {e^{ - 4}}}}{2}} \right)\) \( \times 1000 \approx \) \(3307,188\)
Donc \({A_1} = 3307,188\) m2
Calculons le coût de ce terrain entier.
\(\ln \left( {\frac{{{e^4} + {e^{ - 4}}}}{2}} \right)\) \( \times 2000000\) \( \approx 6614376\) F
Tâche 2 : Déterminons le montant qu'aura ABBA s'il ne souhaite vendre que la portion réservée aux pastèques.
Calculons en m2 l'aire \({A_2}\) de la portion réservée aux pastèques.
\({A_2} = \) \(\left( {\int_0^4 {\left( {\frac{{{e^x} - {e^{ - x}}}}{{{e^x} + {e^{ - x}}}} - \frac{1}{4}x} \right)} } \right)\) \( \times 10000 \approx \) \(1307,488\) m2
Calculons le montant pour cette portion réservée aux pastèques.
\(\left( {\ln \left( {\frac{{{e^4} + {e^{ - 4}}}}{2}} \right) - 2} \right)\) \( \times 2000000 \approx \) \(2614376\)
Tâche 3 : Aidons ABBA à retrouver le nombre de sacs de chaque type des deux produits cultivés.
Effectuons le choix des inconnues et procédons à la mise en équations.
Désignons par x et y les nombres de sacs de pastèques et de carottes respectivement.
Nombre total de sacs : \(x + y = 17\)
A la fin de la vente : \(6800\left( {x - 1} \right)\) \( - 3000\left( {y - 1} \right)\) \( = 4000\)
Résolvons le système obtenu nous permet d’avoir : \(\left\{ \begin{array}{l}x = 6\\y = 11\end{array} \right.\)
Donc 6 sacs de pastèques et 11 sacs de carottes.
NB : Le nombre 17 n'étant pas visible sur l'épreuve (confondu à 47) d'une part et l’expression « différence entre…. » d'autre part, accepter aussi l'un des systèmes ci-après :
\(x + y = 17\) et \( - 6800\left( {x - 1} \right)\) \( + 3000\left( {y - 1} \right)\) \( = 4000\) soit
\(\left\{ \begin{array}{l}x + y = 17\\ - 34x + 15y = 1\end{array} \right.\)
Ou \(x + y = 47\) et \(6800\left( {x - 1} \right) - \) \(3000\left( {y - 1} \right)\) \( = 4000\) soit \(\left\{ \begin{array}{l}x + y = 47\\34x - 15y = 39\end{array} \right.\)
Ou \(x + y = 47\) et \( - 6800\left( {x - 1} \right)\) \( + 3000\left( {y - 1} \right)\) \( = 4000\) soit \(\left\{ \begin{array}{l}x + y = 47\\ - 34x + 15y = 1\end{array} \right.\)
Et ces trois derniers systèmes ont respectivement pour couples solutions \(\left( {\frac{{254}}{{49}};\frac{{579}}{{49}}} \right)\) , \(\left( {\frac{{744}}{{49}};\frac{{1559}}{{49}}} \right)\) ou \(\left( {\frac{{704}}{{49}};\frac{{1599}}{{49}}} \right)\) et dans ces trois derniers cas, le problème posé n'a pas de solution.
Commentaires
Enregistrer un commentaire