ENNONCE
Exercice l : Mouvement dans les champs de forces / 6 points
Partie A : Mouvement d'un solide sur une gouttière / 3 points
Un solide (S) de masse m, assimilable à un point matériel, glisse dans une gouttière comprenant une partie AB rectiligne et horizontale, et une partie circulaire BC de centre \(\Omega \) et de rayon r = 1,0 m. La partie circulaire est tangente en B à la partie rectiligne AB. Le solide est lancé dans la gouttière en A avec une vitesse initiale parallèle à la section AB de la gouttière et de module \({v_A} = 10\) m/s. On donne : m = 200g ; \(\alpha = {60^o}\) ; g = 10 m/\({s^2}\). On admet que le contact entre le solide et la gouttière se fait sans frottements.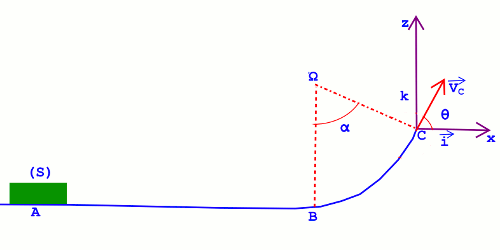 1. Donner en justifiant par l’énoncé de la loi qui fonde votre raisonnement, la valeur de la vitesse du solide (S) en B. 0,75 pt
1. Donner en justifiant par l’énoncé de la loi qui fonde votre raisonnement, la valeur de la vitesse du solide (S) en B. 0,75 pt
2. En appliquant la deuxième loi de Newton au solide, déterminer la valeur F de l’action de la gouttière sur le solide en C. On admettra que la valeur de la vitesse du solide en C vaut \({v_C} = 9\) m/s.
3. La vitesse \({\overrightarrow v _C}\) du solide en C fait un angle \(\theta = {60^o}\) avec l’horizontale.
Établir dans le repère \(\left( {C;\overrightarrow i ,\overrightarrow k } \right)\), l’expression littérale de l’équation cartésienne de la trajectoire du solide après le point C. On prendra pour instant initial, l’instant de passage du solide en C. 1,25 pt
Partie B : Particule chargée dans un champ électrique ou magnétique /3 points
Un tube dans lequel on a fait un vide poussé, contient deux plaques métalliques verticales, planes et parallèles, P et Q, distantes de d = 2,5 cm. On établit une différence de potentiel de valeur constante U= 1000 V entre les plaques, Q étant au potentiel le plus élevé.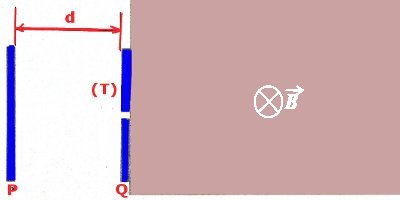 1. Sur la figure ci-dessus à remettre avec la copie, représenter le vecteur champ électrostatique entre les plaques ; puis calculer son module E. 0,75 pt
1. Sur la figure ci-dessus à remettre avec la copie, représenter le vecteur champ électrostatique entre les plaques ; puis calculer son module E. 0,75 pt
2. Chauffée, la plaque P émet des électrons, avec une vitesse initiale qu’on supposera nulle. On négligera le poids de l’électron par rapport aux autres forces.
2.1 Donner les caractéristiques (direction, sens et intensité) de la force électrostatique qui s’applique entre les plaques sur un électron émis par P. 0,75 pt
2.2 Calculer la valeur de la vitesse d’un électron à l’arrivée sur la plaque Q. 0,75 pt
3. La plaque Q est percée d’un trou (T) qui laisse passer des électrons. Au-delà de cette plaque, les électrons sont soumis à un champ magnétique uniforme de valeur B.
Compléter la figure ci-dessus à remettre avec la copie en esquissant la trajectoire d’un électron dans le champ magnétique; puis caractériser cette trajectoire à l'aide d’une distance. 0,75 pt
On donne : charge électron : \( - e = \) \( - 1,6 \times {10^{ - 19}}\) C; \({m_e} = \) \(9,1 \times {10^{ - 31}}\) kg ; \(B = 1,25 \times {10^{ - 3}}\) T
Exercice 2 : Systèmes oscillants / 6 points
Partie A : Oscillations électriques forcées / 3 points
Un circuit comprenant en série un conducteur ohmique de résistance R = 300 \(\Omega \) et un condensateur de capacité C, est branché aux bornes d’un générateur de basses fréquence (GBF).
1. On se propose d’observer sur la voie 1 d’un oscilloscope bicourbe, les variations de la tension d'excitation \(u(t)\) délivrée par le (GBF), et sur la voie 2 celles de la tension \({u_R}(t)\) aux bornes du conducteur ohmique.
Faire un schéma de branchement.
2. On obtient les oscillogrammes ci-dessous avec les réglages suivants :
Sensibilité verticale sur les deux voies: 1V/div.
Balayage 5 ms/div.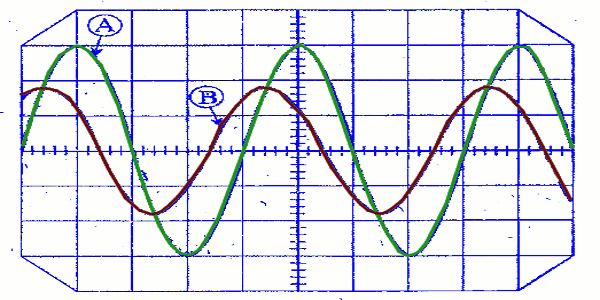 1. indiquer, en justifiant la réponse, pour chacune des courbes la voie correspondante de l’oscilloscope 0,5 pt
1. indiquer, en justifiant la réponse, pour chacune des courbes la voie correspondante de l’oscilloscope 0,5 pt
2. Déterminer :
2.1. La fréquence N de la tension délivrée parle (GBP) ;
2.2 La valeur efficace I de l’intensité du courant qui traverse le circuit ; 0,5 pt
2.3. L’impédance du circuit; 0,5 pt
2.4. La capacité du condensateur.
Partie B : Étude énergétique d’un oscillateur mécanique / 3 points
Un pendule est constitue d’une boule de masse m de centre d’inertie G, fixée à l’extrémité d’un fil inextensible et de masse négligeable devant celle de la boule. L’autre extrémité du fil est accrochée en un point fixe O. On assimile ce pendule à un pendule simple de longueur L.
Le plan vertical du mouvement du pendule est rapporté à un axe horizontal x‘x et à un axe vertical z’z, d’origine \({G_o}\) position du centre d'inertie à l’équilibre, orientés comme l’indique la figure ci-dessous. On s’intéresse aux petites oscillations du pendule et on néglige les frottements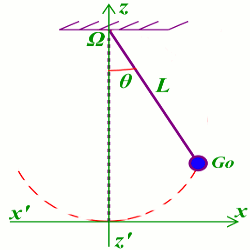 On donne : L = 41 cm, m = 236 g et g = 9,8 m/\({s^2}\)
On donne : L = 41 cm, m = 236 g et g = 9,8 m/\({s^2}\)
1. L’etude étant faite pour les oscillations de faible amplitude, on peut écrire :
\(\sin (\theta ) \approx \theta \), \(1 - \cos (\theta )\) \( \approx \frac{{{\theta ^2}}}{2}\) (\(\theta \) en radians).
1.1. Montrer que \(\theta = \frac{x}{L}\) où x est l'abscisse de G sur l’axe x’x. 0,25 pt
1.2. Exprimer l'énergie potentielle de pesanteur Epp du "système {pendule terre} en fonction de x. On prendra Epp = 0 lorsque G est en Go. 0,75 pt
1.3. Montrer que l’énergie mécanique totale du système précédent s’écrit : \({E_m} = \frac{{mgx_m^2}}{{2L}}\), ou \({x_m}\) est l’abscisse maximale de G sur l’axe x’x. 0,5 pt
La figure ci-dessous donne les variations des différentes énergies du pendule en fonction de l’abscisse x du centre d’inertie de la boule pendule.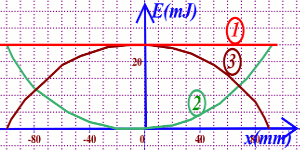 2.1 Attribuer à chaque courbe de la figure l’énergie correspondante. 0,75 pt
2.1 Attribuer à chaque courbe de la figure l’énergie correspondante. 0,75 pt
2.2 Calculer la valeur de la vitesse maximale de la masse du pendule. 0,75 pt
Exercice 3 : Phénomènes ondulatoires et corpusculaires / 4 points
Partie A : Ondes mécaniques à la surface de l’eau / 2 points
L’extrémité S d’une tige verticale impose à la surface de l’eau d’une cuve, des vibrations transversales sinusoïdales de fréquence f = 100 Hz et d’amplitude a = 2 mm, qui se propagent à la célérité c = 0,6 m/s. On supposera qu’il n’y a ni réflexion, ni amortissement de l’onde.
1. On éclaire la surface de l’eau avec un Stroboscope dont la fréquence des éclairs est légèrement inférieure à 100 Hz. Qu’observe-t-on ? 0,5 pt
2. Écrire l’équation horaire du mouvement de S, en choisissant comme origine des temps l’instant où S passe par sa position d'équilibre O, en se déplaçant vers le haut. O sera pris comme origine des élongations, comptées positivement vers le haut. 0,5 pt
3. Écrire l’équation horaire du mouvement d'un point M de la surface de l'eau, situé à la distance d = 1,5 cm de O. Comparer les mouvements de M et de S.
Partie B : Radioactivité / 2 points
Peur vérifier la forme ou le fonctionnement de la glande thyroïde, on procède à une scintigraphie thyroïdienne en utilisant de l’iode 131. Un patient en ingère une masse m = 1,00 \(\mu g\).
1. Déterminer le nombre No d’atomes radioactifs (donc de noyaux radioactifs) initialement présents dans la dose ingérée. L’instant de l’ingestion est pris pour origine des dates (t = 0 s).
2. L’iode 131 est radioactif \({\beta ^ - }\).
Écrire l’équation bilan de sa désintégration. On admettra que le noyau fils n'est pas produit dans un état excité. 0,5 pt
On donne le symbole et le numéro atomique de quelques éléments chimiques :
| Antimoine (Sb) | Tellure (Te) | Iode (I) | Xénon (Xe) | Césium (Cs) |
| Z = 51 | Z = 52 | Z = 53 | Z = 54 | Z = 55 |
3. La demi-vie T de l’iode l3l vaut 8,0 jours.
Définir la demi-vie (ou période radioactive) d’un échantillon radioactif. 0,5pt
4. Donner l’expression littérale de l’activité Ao de l’échantillon à l’origine des dates, en fonction de No et de T.
Calculer sa valeur numérique. 0,5 pt
Données : Constante d’Avogadro : NA = \(6,02 \times {10^{23}}\) /mol. Masse molaire atomique de l’isotope 131 de l‘iode : M = 131 g/mol.
Exercice 4 : Exploitation des résultats d’une expérience / 4 points
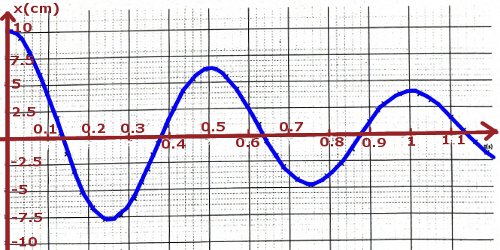
Un solide (S) de masse m, mobile sur un plan horizontal, est relié à l’une des extrémités d’un ressort à spires non jointives de raideur k et de masse négligeable, dont l'autre extrémité est fixe. Écarté de sa position d'équilibre dans la direction de l’axe du ressort, puis lâché sans vitesse initiale, le solide effectue des oscillations parallèlement à la direction précédente. On repère le solide au cours du temps par l’abscisse x de son centre d’inertie G, sur l’axe x’x, parallèle à l’axe du ressort et dont l’origine est Go, la position de G à l’équilibre (figure). La figure 7 de l'annexe à remettre avec la copie, est la représentation des variations de l’abscisse x en fonction du temps.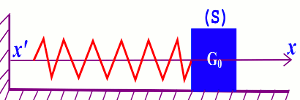 1. Donner une interprétation énergétique de la diminution progressive de l’amplitude des oscillations. 0,5 pt
1. Donner une interprétation énergétique de la diminution progressive de l’amplitude des oscillations. 0,5 pt
2. Représenter sur un schéma, les forces extérieures qui s’appliquent sur le solide (S), lorsqu’il passe par une position (l’abscisse x positive, en allant dans le sens positif de l’axe x’x). 0,75 pt
3. Déterminer à l’aide du graphe, la pseudo période T des oscillations, puis en déduire la raideur k du ressort, sachant que m = 250 g. 1,5 pt
4. Représenter en justifiant, sur la figure ci-dessous à remettre avec la copie, pour 0 < t < 0,8 s l’allure de la courbe donnant les variations de l’énergie mécanique Em de l’oscillateur en fonction du temps. On prendra k = 40 N/m. 0,75 pt
CORRECTION
Exercice I Mouvements dans un champ de forces
Partie A Mouvement d’un solide sur une gouttière
1. Le contact entre le solide et la gouttière se faisant sans frottement, nous pouvons y appliquer le principe d’inertie qui stipule que : Dans un référentiel galiléen, le centre d’inertie d’un système isolé ou pseudo-isolé est soit au repos, soit en mouvement rectiligne uniforme. 0,25 x 3 = 0,75 pt
2. Déterminons l’intensité de la force F, l’action de la gouttière sur le solide sur le mobile
Dans le référentiel de laboratoire supposé galiléen, nous avons : 1 pt
\(\overrightarrow F + \overrightarrow P \) \( = m\overrightarrow {{a_G}} \)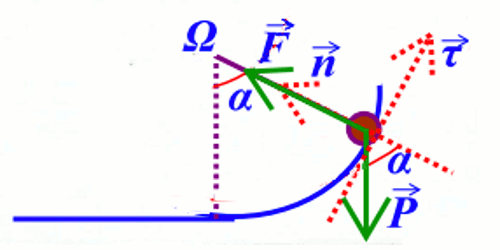 • Suivant le vecteur unitaire normale \(\overrightarrow n \), nous avons :
• Suivant le vecteur unitaire normale \(\overrightarrow n \), nous avons :
\(F - P\cos \alpha \) \( = m{a_n}\) avec \(P = mg\) et \({a_n} = \frac{{v_C^2}}{r}\), soit :
\(F = m(g\cos \alpha \) \( + \frac{{v_C^2}}{r})\)
AN : \(F = 17,2N\)
3. Equation cartésienne de la trajectoire du mobile (S) à partir de C. 0,25 x 3 = 0,75 pt
Apres le point C, (S) n’est plus soumis qu’à l’action de son poids, Dans le référentiel de laboratoire supposé galiléen, appliquons le TCI 1,25 pt
\(\sum {\overrightarrow F ext} \) \( = m\overrightarrow {{a_G}} \Leftrightarrow \) \(\overrightarrow P = m\overrightarrow g = \) \(m\overrightarrow {{a_G}} \) soit \(\overrightarrow g = \overrightarrow {{a_G}} \).
Dans le référentiel \((C;\overrightarrow i ,\overrightarrow j )\), on a :
\(\overrightarrow {{a_G}} \left( \begin{array}{l}0\\ - g\end{array} \right)\),
\(\overrightarrow {{v_C}} \left( \begin{array}{l}{v_C}\cos \alpha \\{v_C}\sin \alpha \end{array} \right)\)
\(C\left( \begin{array}{l}0\\0\end{array} \right)\)
\(\overrightarrow {{v_G}} \left( \begin{array}{l}{v_C}\cos \theta \\ - gt + {v_C}\sin \theta \end{array} \right)\)
\(\overrightarrow {CG} \left( \begin{array}{l}{v_C}\cos \theta \\ - \frac{1}{2}g{t^2} + ({v_C}\sin \theta )t\end{array} \right)\).
Soit :
\(z = \) \(\frac{{ - g}}{{2{{\cos }^2}(\theta )v_C^2}}{x^2}\) \( + x\tan \theta \)
Partie B : Particule chargée dans un champ électrique et magnétique
1. Calcule du module E du champ électrique 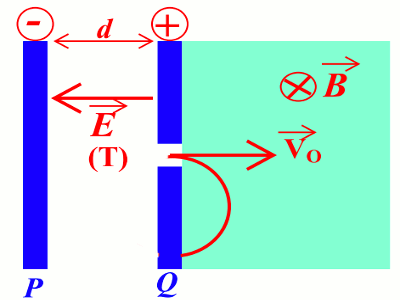 \(E = \frac{U}{d}\) soit \(E = 4 \times {10^4}\) V/m
\(E = \frac{U}{d}\) soit \(E = 4 \times {10^4}\) V/m
2.1 Caractéristiques de la force électrostatique \(\overrightarrow F \) subie par un électron 0,25 x 3 =0,75 pt
• Direction : orthogonale aux plaques P et Q
• Sens : De P vers Q
• Intensité : \(F = qe\) AN : \(F = 6,4 \times {10^{ - 15}}\) N
2.2 Vitesse \(v\) d’un électron à l’arrivée sur la plaque Q 0,75 pt
Entre P et Q, appliquons le Théorème de l’énergie cinétique (TEC) à l’électron soumis à la force électrique, son poids étant négligeable.
\(\Delta {E_C} = \) \(\sum {W(\overrightarrow F ext)} \) soit
\(\frac{1}{2}m{v^2} - 0 = \) \( - e\overrightarrow E .\overrightarrow {PQ} \Leftrightarrow \) \(\frac{1}{2}m{v^2} = \) \( - e\left( {{V_P} - {V_Q}} \right)\)
\({V_Q} - {V_P} = U\) \( \Rightarrow v = \) \(\sqrt {\frac{{2eU}}{m}} \)
AN : \(v = 1,88 \times {10^7}\) m/s
3. Caractérisation de la trajectoire 0,75 pt
Esquisse de la trajectoire (voir image ci-dessus)
Cette trajectoire est un cercle de rayon R. Dans le référentiel terrestre supposé galiléen, l’électron est soumis à la force de Lorentz : \(\overrightarrow F = \) \( - e\overrightarrow v \wedge \overrightarrow B \), le poids de l’électron étant négligeable, Appliquons à l’électron le TCI.
Il vient : \( - e\overrightarrow v \wedge \overrightarrow B = m\overrightarrow a \) \( \Rightarrow \overrightarrow a = \) \(\frac{{ - e\overrightarrow v \wedge \overrightarrow B }}{m}\)
Ainsi : \(\overrightarrow a \bot \overrightarrow B \) \( \Rightarrow \overrightarrow a = \overrightarrow {{a_n}} \) \( \Rightarrow \frac{{evB}}{m}\) \( = \frac{{{v^2}}}{R}\)
D’où \(R = \frac{{mv}}{{eB}}\)
AN : \(R = 8,55 \times {10^{ - 2}}\) m
Exercice II Systèmes oscillants
Partie A : Oscillations électriques forcées
1. Schéma du branchement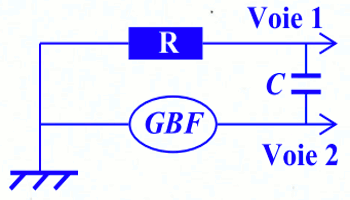 2. Indication de la voie correspondante à chaque courbe 0,5 pt
2. Indication de la voie correspondante à chaque courbe 0,5 pt
A est la courbe de la voie 1 \(u(t)\) et B la courbe de la voie 2 \({u_R}(t)\) car le condensateur provoque un retard de phase de \(u(t)\) par rapport à \(i(t)\)
2.1 Détermination de la fréquence N 0,5 pt
Une période couvre 4 divisions et 1 division représente 5 ms. La période est donc : \(T = 4 \times 5\) \( = 20\) ms
\(N = \frac{1}{T} = 50\) Hz
2.2 Valeur efficace I de l’intensité du curant dans le circuit 0,5 pt
\(I = \frac{{{u_{R(\max )}}}}{{R\sqrt 2 }}\) avec \({{u_{R(\max )}} = 1,8 \times 1}\) \({ = 1,8}\)V et \(R = 300\Omega \) Soit \(I = 4,24 \times {10^{ - 3}}\) A
2.3 L’impédance Z du circuit 0,5 pt
\(Z = \frac{{{U_{eff}}}}{{{I_{eff}}}}\) \( = \frac{{u{{(t)}_{\max }}}}{{i{{(t)}_{\max }}}}\)
Avec \({u{{(t)}_{\max }} = 3}\) V et \({i{{(t)}_{\max }} = }\) \({6 \times {{10}^{ - 3}}}\) A soit \(Z = 500\Omega \)
2.4 Calcule de la capacité du condensateur 0,5 pt
\(Z = \) \(\sqrt {{R^2} + {{\left( {\frac{1}{{2\pi NC}}} \right)}^2}} \) \( \Rightarrow C = \) \(\frac{1}{{2\pi N\sqrt {{Z^2} - {R^2}} }}\)
\(C = \) \(7,96 \times {10^{ - 6}}\) F
Partie B : Étude énergétique d’un oscillateur mécanique
1.1 Montrons que \(\theta = \frac{x}{L}\)
En fait, \(\sin \theta = \frac{x}{L}\), avec \(\sin \theta \approx \theta \) alors \(\theta = \frac{x}{L}\)
1.2 Expression de l’énergie potentielle de pesanteur Epp 0, 75 pt
\(Epp = mgh\) avec \(h = \) \(L - L\cos \theta = \) \(L(1 - \cos \theta )\) \( = \frac{{L{\theta ^2}}}{2}\) \( = \frac{{{x^2}}}{{2L}}\)
\(Epp = \frac{{mg}}{{2L}}{x^2}\)
1.3 Montrons que l’énergie mécanique \(Em = \frac{{mg}}{{2L}}X_M^2\)
En effet, \(Em = Ec + Epp\)
Les frottements étant négligeables, le système est conservatif
Lorsque \(x = Xm\), \(\dot \theta = 0\) et Ec = 0. On a alors \(Em = Epp\) \( = \frac{{mg}}{{2L}}X_M^2\).
2.1 Énergie correspondant à chaque courbe
• correspond à l’énergie mécanique
• correspond à l’énergie potentielle
• correspond à l’énergie cinétique
2.2 Calcule de la vitesse maximale de la masse du pendule 0,75 pt
\({E_{C\max }} = \) \(\frac{1}{2}mv_{c\max }^2\) \( \Rightarrow {v_{C\max }} = \) \(\sqrt {\frac{{2{E_{C\max }}}}{m}} \)
Avec \({E_{C\max }} = 25\) mJ, on a : \({v_{C\max }} = 0,46\) m/s
Exercice III Phénomènes ondulatoires et corpusculaires
Partie A : Ondes mécaniques à la surface de l’eau
1. Faits observés 0,5 pt
On observe une succession de rides circulaires prendre naissance au point d’impact de la tige sur l’eau et s’agrandir lentement.( Mouvement ralenti dans le sens réel)
2. Équation horaire de S 0,5 pt
\({y_s} = \) \(a\sin (2\pi ft + \varphi )\)
\(\left\{ \begin{array}{l}{y_s}(0) = 0\\y{'_s}(0) \succ 0\end{array} \right.\) \( \Rightarrow \) \(\left\{ \begin{array}{l}a\sin (\varphi ) = 0\\\cos (\varphi ) \succ 0\end{array} \right.\) \( \succ \varphi = 0\)
\({y_s} = 2 \times {10^{ - 3}}\) \(\sin (200t)\) avec ys en mètres
3. Équation horaire du mouvement du point M 1 pt
\({y_M} = \) \({y_S}(t - \frac{d}{v})\)
\({y_M} = 2 \times {10^{ - 3}}\) \(\sin (200\pi t - \) \(\frac{{200\pi d}}{v}) = \) \(2 \times {10^{ - 3}}\sin (200\pi t\) \( - 5\pi )\)
On constate que S et M sont en opposition de phase
Partie B Radioactivité
1. Calcule de No 0,5 pt
La quantité de matière d’iode 131 dans l’échantillon est telle que : \(n = \frac{m}{M} = \) \(\frac{{No}}{{{N_A}}}\) alors : \(No = \frac{{m \times {N_A}}}{M}\)
Soit \(No = 4,6 \times {10^{15}}\) noyaux
2. Équation bilan de la désintégration 0,5 pt
\({}_{53}^{131}I \to \) \({}_{54}^{131}Xe + {}_{ - 1}^0e\)
3. Définition de la demi-vie d’un échantillon radioactif 0,5 pt
C’est temps nécessaire pour que la moitie des noyaux radioactifs initialement présents dans un échantillon se désintègrent.
4. Expression littérale de l’activité Ao 0,5 pt
\(Ao = No\frac{{\ln 2}}{T}\)
AN: \(Ao = \) \(4,6 \times {10^9}Bq\)
Exercice IV Exploitation des résultats d’une expérience
1. Interprétation énergétique de la diminution de l’amplitude 0,5 pt
Cette diminution d’amplitude est due à une diminution progressive de l’énergie mécanique conséquence de l’existence des forces de frottements sur le solide (S)
2. Représentation des forces 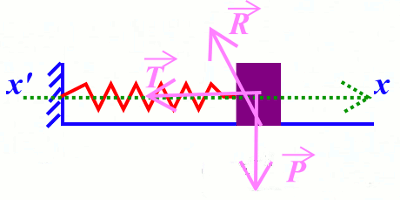 3. Pseudo-période T des oscillations
3. Pseudo-période T des oscillations
\(T = 0,5\)
Calcule de la constance de raideur k
\(T = 2\pi \sqrt {\frac{m}{k}} \) \( \Rightarrow k = \) \(\frac{{4{\pi ^2}m}}{{{T^2}}}\)
AN : \(k = 39,48\) N/m
4. Représentation de Em 0,5 pt
Pour une amplitude Xm donnée, \(Em = \frac{1}{2}kX_m^2\) avec Xm (m), Em (J)
Traçons la courbe 0,5 pt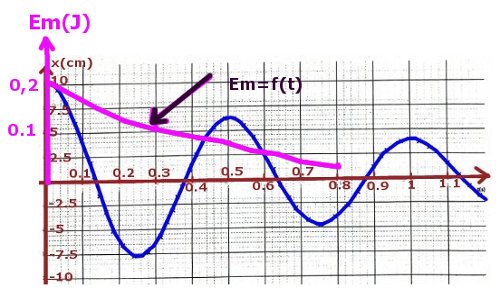
Commentaires
Enregistrer un commentaire