ENNONCE
Exercice 1 : Mouvement dans les champs de forces / 6 points
L exercice comporte deux parties indépendantes.
Partie A Champ de gravitation / 2 points
On assimile la Terre à un corps à répartition sphérique de masse, de centre O, de rayon RT = 6 380 km, et de masse MT = 593x1024 kg.
Prendre G (Constante gravitationnelle ) = 6,67 x 10-11 USI.
1. Écrire l’expression de la valeur du champ de gravitation à une distance r du centre de la Terre. 0,5 pt
2 Un satellite de mS = 360 kg évolue à une distance r = 42 O00 km du centre de la Terre.
Donner les caractéristiques de la force de gravitation qui s’exerce sur ce satellite. 0,75 pt
3 Faire un schéma représentant, la Terre, le satellite sur son orbite et quelques lignes du champ de gravitation.
Donner la qualification d’orientation de ce champ 0,75 pt
Partie B Champs électrique et magnétique / 4 points
Dans le dispositif schématisé sur la figure ci-dessous, des ions positifs de masse m, de charge q sortent en I d’une chambre d’ionisation avec une vitesse négligeable. Ils sont accélérés entre l et F par une tension U = VI — VF, continue et réglable. Ces ions sont ensuite déviés entre S et P par un champ magnétique uniforme de vecteur \(\overrightarrow B \) perpendiculaire au plan de la figure, la valeur B du champ magnétique restant constante pendant toute la durée d’utilisation. À la sortie du champ magnétique, les ions sont recueillis à l'entrée C d’un collecteur.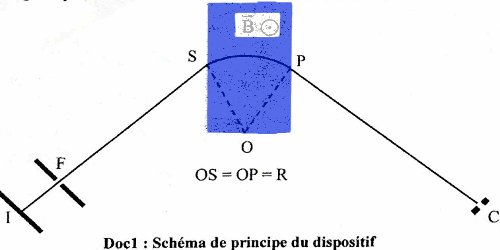 Tous les ions que l'on veut recueillir en C doivent suivre la même trajectoire IFSPC. D’autre part le vide est réalisé dans l’appareil, et l’effet de la pesanteur sur les ions est négligeable. La portion SP est un arc de cercle de centre O et de rayon R.
Tous les ions que l'on veut recueillir en C doivent suivre la même trajectoire IFSPC. D’autre part le vide est réalisé dans l’appareil, et l’effet de la pesanteur sur les ions est négligeable. La portion SP est un arc de cercle de centre O et de rayon R.
1. Déterminer combien de phases comporte le mouvement des ions sur la trajectoire qui leur est imposée ; préciser quelles sont celles de ces phases qui sont des mouvements uniformes. 0,5pt
2. Établir en fonction de q, m, et U l’expression de la vitesse avec laquelle un ion quelconque du faisceau parvient en S. 0,5 pt
3. Établir une relation entre q, v, B, m, et R lorsque que cet ion suit la trajectoire imposée. 0.5 pt
4. Déduire des deux questions précédentes une relation entre q, B, R, m, et U. 0,5 pt
On utilise le dispositif pour identifier les isotopes de l’indium : les atomes d’indium s’ionisent sous la forme d’ions \(I{n^{2 + }}\).
5.1. On place d’abord dans la chambre de l’indium 115.
Calculer la valeur à donner à la tension U pour que les ions d’indium 115 soient collectés en C. 1 pt
On donne R=0,70m ; B =0,16T;
Masse d’un atome d’indium 115 : 114,90 u (1 u = 1,66x10-27 kg) ;
Charge électrique élémentaire : e = 1,6x10-19 C.
5.2. On place maintenant dans la chambre d’ionisation un mélange d’isotopes d’indium. Pour les recueillir successivement en C, il faut donner à U différentes valeurs comprises entre 17919 V et 24 942 V, B et R gardant la même valeur.
Déterminer l’intervalle dans lequel se situent les nombres de masse de ces isotopes. 1 pt
Exercice 2 :Systèmes oscillants / 6 points
Partie A: Stroboscopie / 1 point
1. Définir : phénomène périodique. 0,25 pt
2. Sur un disque noir est peint un rayon blanc. La fréquence de rotation du disque est N = 28 tr/s. Ce disque est éclairé par des éclairs dont la fréquence Ne peut varier de 10 Hz à 100 Hz.
Déterminer pour quelles fréquences des éclairs, le disque paraît immobile avec trois rayons blancs. 0.75 pt
Partie B : Oscillateur mécanique / 2,5 points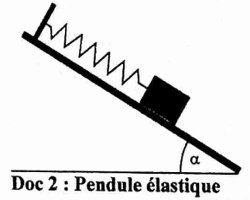
Un ressort (R) de masse négligeable et à spires non jointives a une extrémité A accrochée à un support fixe et l’autre B à un solide (S) de masse m = 576 g pouvant évoluer sans frottement sur la ligne de plus grande pente d'un plan incliné d’un angle α sur l'horizontale. La longueur à vide du ressort est L0 = 16 cm et lorsque le solide (S) est accroché, la longueur à l’équilibre du ressort vaut L1 = 19,6 cm. 0n donne g = I0 m/s2 ; α = 30o
1. Calculer la constante de raideur k du ressort. On tire le solide (S) vers le bas d’une longueur a = 4 cm puis on le lâche à une date prise comme origine des dates, sans vitesse initiale.
2.1. Établir l’équation différentielle qui régit le mouvement ultérieur du solide. 0,75 pt
2.2. Calculer la pulsation propre \({\omega _0}\) de l’oscillateur. 0,5 pt
2.3. Écrire l'équation horaire du mouvement en tenant en compte des conditions initiales.
Partie C : Oscillateurs électriques / 2,5 points
On associe à une bobine de résistance r = 220 Ω et d’inductance L = 349 mH, un conducteur ohmique de résistance R = 780 Ω. Ce circuit est parcouru par un courant alternatif sinusoïdal de fréquence N = 240 Hz.
1.1. Faire la construction de Fresnel relative à l’impédance Z de ce circuit puis calculer sa valeur. On arrondira la valeur à l’unité.
1.2. Écrire l’expression de la valeur instantanée u(t) de la tension aux bornes du circuit en prenant pour référence des phases l’intensité du courant.
On constitue un deuxième circuit en associant les éléments précédents à un condensateur de capacité C. L’ensemble est alimenté par un générateur de basses fréquences (GBF). Un oscilloscope à deux voies branché aux points M, N et P de ce circuit (voir schéma du circuit). Il permet de visualiser les tensions u1=uPM et u2=uNM. Les réglages sont les suivants :
vitesse de balayage: 20ms/div. (1 ms = 10-3 s) ;
gain vertical: 2V/div en voie 1.
On obtient l’oscillogramme de la figure ci dessous.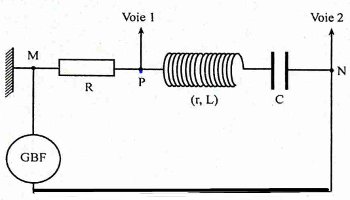 2.1. Nommer le phénomène mis en évidence par cet oscillogramme. 0,25 pt
2.1. Nommer le phénomène mis en évidence par cet oscillogramme. 0,25 pt
2.2. Mesurer à partir de l’oscillogramme la fréquence caractéristique NC du phénomène
2-3- Calculer la Valeur de la capacité C du condensateur utilisé. 0,75 pt
Exercice 3 : Phénomènes corpusculaires et ondulatoires / 4 points
Partie A : Étude d'une cellule photoélectrique / 2 points
Une source F émettant deux lumières monochromatiques de longueur d’onde respectives \({\lambda _1} = 500nm\) et \({\lambda _1} = 500nm\) , éclaire une cellule photoélectrique.
1. Faire un schéma annoté du dispositif expérimental permettant de tracer la caractéristique tension-intensité d’une cellule photoélectrique 0,5 pt
2. L’énergie d’extraction d'un électron de la cathode est W0 = 2,25 eV pour la cellule photo électrique que considérée.
Montrer qu’une seule des lumières monochromatiques ci-dessus produit l’effet photoélectrique. 0,5pt
On donne: h(Constante de Planck) = 6 63x10-34 Js
C(Célérité de la lumière) = 3.00x 108 m/s ; e(Charge d’un proton) = l,60xl0- 19 C; me
me (Masse d’un électron)= 9,1 1 x 10-31 kg
3. Déterminer la vitesse maximale Vmax des électrons émis par la cathode. 0,5 pt
4. Calculer la valeur du potentiel d’arrêt US de cette cellule photo émissive. 0,5 pt
Partie B: Désintégration radioactive de l'uranium 238 / 2 points
La désintégration de l’uranium 238 est de type α et conduit à un noyau de Thorium (Th).
1. Ecrire l’équation de cette réaction nucléaire. 0.5 pt
2. La demi-vie de l’uranium 238 est \({t_{\frac{1}{2}}} = 4,5 \times {10^9}ans\). Définir le terme demi-vie. 0,5 pt
3. Calculer la masse m d'uranium 238 qui reste au bout de 10 ans dans un échantillon de masse initiale m0 = 1 g. 1 pt
Exercice 4 Exploitation des résultats d'une expérience / 4 points
Au cours de L’expérience décrite par le schéma ci-dessous, on a obtenu les résultats rassemblés dans le tableau ci-dessous.
| N(Hz) | 0,25 | 0,84 | 1,03 | 1,12 | 1,19 | 1,23 | 1,25 | 1,26 |
| Xm(cm) | 0,2 | 1,2 | 2,6 | 4,0 | 6,6 | 11,4 | 13,0 | 13,8 |
| N(Hz) | 1,27 | 1,29 | 1,33 | 1,50 | 1,63 | 1,82 | 2,24 |
| Xm(cm) | 14,1 | 12,9 | 9,0 | 3,3 | 2,2 | 1,6 | 1,1 |
N est la fréquence de l’excentrique entraîné par le moteur. Xm. est l'amplitude des oscillations du solide suspendu au ressort.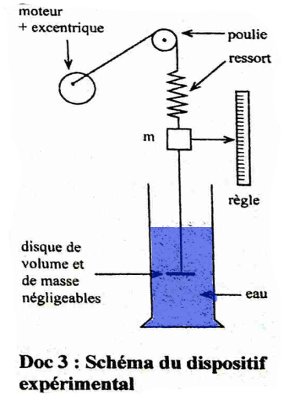
1. Quel est le type d’oscillations observées au cours de cette expérience ? Préciser l’excitateur et le résonateur. 0,75 pt
2. Représenter sur la feuille à remettre le graphe donnant l’amplitude Xm en fonction de la fréquence N.
Échelle: l cm pour 0,2 Hz; l cm pour 1 cm. 1,75 pt
3. Déterminer le phénomène physique mis en évidence par ce graphique. 0,25 pt
A l’aide du graphique, déterminer :
4.1. La largeur \(\Delta N\) de la bande passante. 0,5 pt
4.2. La valeur de la fréquence propre No du résonateur. 0,25 pt
5. La masse du solide accroché au ressort est m = 216 g. Déterminer la valeur de la constante de raideur K du ressort. 0,5 pt
Commentaires
Enregistrer un commentaire